
|
Resolución de Ecuaciones y Sistemas de Ecuaciones |
|||||||||||
Ecuaciones de 1º grado (#1) |
|||||||||||
Ecuaciones de 2º grado (#2) |
|||||||||||
Ecuaciones de 3º grado o superior (#3)
|
Ecuaciones Bicuadradas (#4)
|
Ecuaciones Racionales (#5)
| Ecuaciones Irracionales (#6)
|
Ecuaciones Exponenciales (#7)
|
Ecuaciones Logarítmicas (#8)
|
Sistemas de Ecuaciones Lineales (#9)
|
Sistemas de Ecuaciones No Lineales (#10)
|
Sistemas de Ecuaciones Exponenciales (#11)
|
Sistemas de Ecuaciones Logarítmicas (#12)
|
Algunos resultados teóricosEcuaciones de 2º gradoDada la ecuación \( ax^2+bx+c=0 \) con soluciones \( x_1 \) y \( x_2 \): $$ \mathbf{\hbox{ (Descomposición factorial) }} \left.\begin{array}{l} ax^2+bx+c = a(x-x_1)(x-x_2)\\ \end{array}\right. $$ $$ \mathbf{\hbox{ (Suma y producto de las soluciones) }} \left\{\begin{array}{l} S = x_1 + x_2 = -\frac{b}{a}\\ P = x_1 \cdot x_2 = \frac{c}{a}\\ \end{array}\right. $$ $$ \left\{\begin{array}{l} ax^2+bx+c = a(x-x_1)(x-x_2) \hbox{ (Dividiendo por a) } \Rightarrow\\ \Rightarrow x^2 + \frac{b}{a}x + \frac{c}{a} = (x-x_1)(x-x_2) = x^2 -x_2x - x_1x + x_1x_2 = x^2 -(x_1 + x_2)x + x_1x_2 \Rightarrow\\ \Rightarrow x^2 + \frac{b}{a}x + \frac{c}{a} = x^2 -(x_1 + x_2)x + x_1x_2 \hbox{ (Igualando coeficientes) } \Rightarrow \left\{\begin{array}{l} x_1 + x_2 = -\frac{b}{a}\\ x_1 \cdot x_2 = \frac{c}{a}\\ \end{array}\right.\\ \end{array}\right. $$ $$ \mathbf{\hbox{ (Solución general Ecuación 2º grado) }} ax^2+bx+c = 0 \Leftrightarrow x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} $$ $$ \left\{\begin{array}{l} ax^2+bx+c = 0 \hbox{ (Dividiendo por a) } \Rightarrow\\ \Rightarrow x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \Rightarrow x^2 + \frac{b}{a}x = - \frac{c}{a} \hbox{ (Completando cuadrados) } \Rightarrow\\ \Rightarrow x^2 + 2\frac{b}{2a}x = - \frac{c}{a} \Rightarrow x^2 + 2\frac{b}{2a}x + \left ( \frac{b}{2a}\right )^2 = - \frac{c}{a} + \left ( \frac{b}{2a}\right )^2 \Rightarrow\\ \Rightarrow x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} = - \frac{c}{a} + \frac{b^2}{4a^2} \Rightarrow \left (x+ \frac{b}{2a} \right )^2 = \frac{b^2 -4ac}{4a^2} \hbox{ (Tomando raíz cuadrada) } \Rightarrow\\ \Rightarrow \sqrt{\left (x + \frac{b}{2a} \right )^2} = \sqrt{\frac{b^2 -4ac}{4a^2}} \Rightarrow x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 -4ac}}{2a} \hbox{ (Despejando x) } \Rightarrow\\ \Rightarrow x = - \frac{b}{2a} \pm \frac{\sqrt{b^2 -4ac}}{2a} \Rightarrow x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}\\ \end{array}\right. $$Factorización de polinomios de 3º grado o superiorDado el polinomio \(P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_2x^{2}+a_{1}x+ a_0:\) $$ \left\{\begin{array}{l} \mathbf{\hbox{ (Valor numérico de } P(x) \hbox{ en } x=x_0)} \left.\begin{array}{l} P(x_0) = a_nx_0^n + a_{n-1}x_0^{n-1} + \cdots + a_2x_0^2 + a_1x_0 + a_0\\ \end{array}\right.\\ \mathbf{\hbox{ (Raíz de un polinomio) }} \left.\begin{array}{l} x_0 \hbox{ raíz de P(x)} \Leftrightarrow P(x_0)=0\\ \end{array}\right.\\ \mathbf{\hbox{ (Teorema del resto) }} \left.\begin{array}{l} \hbox{El resto de la división } P(x):(x \pm x_0) \hbox{ es } P(\mp x_0)\\ \end{array}\right.\\ \mathbf{\hbox{ (Teorema del factor) }} \left.\begin{array}{l} x_0 \hbox{ raíz de } P(x) \Leftrightarrow (x-x_0) \hbox{ factor de } P(x)\\ \end{array}\right.\\ \mathbf{\hbox{ (Regla de Ruffini) }} \left.\begin{array}{l} \hbox{ Se usa para realizar de forma sencilla divisiones de la forma } P(x):(x \pm x_0)\\ \end{array}\right.\\ \end{array}\right. $$
\(P(x):(x+x_0)\)
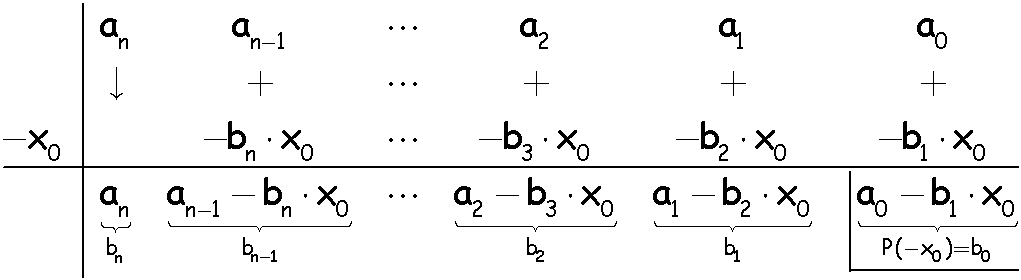
\(P(x):(x-x_0)\) 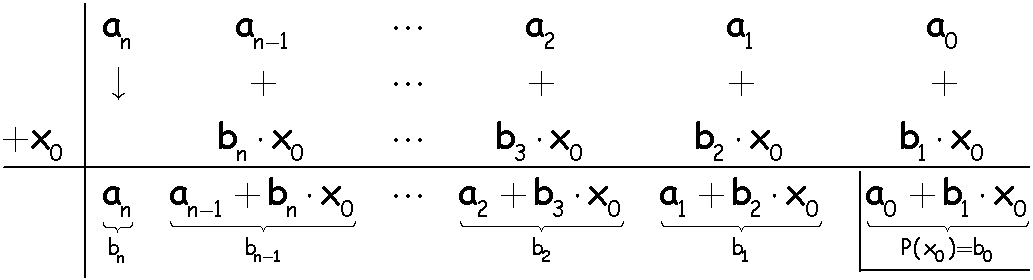
|
|