
|
|
|
|
Propuesta de problemas 2º BACH CCSS PEvAU 2020: Integral indefinida e integral definida. Aplicaciones de la integral
|
Problema (#1)
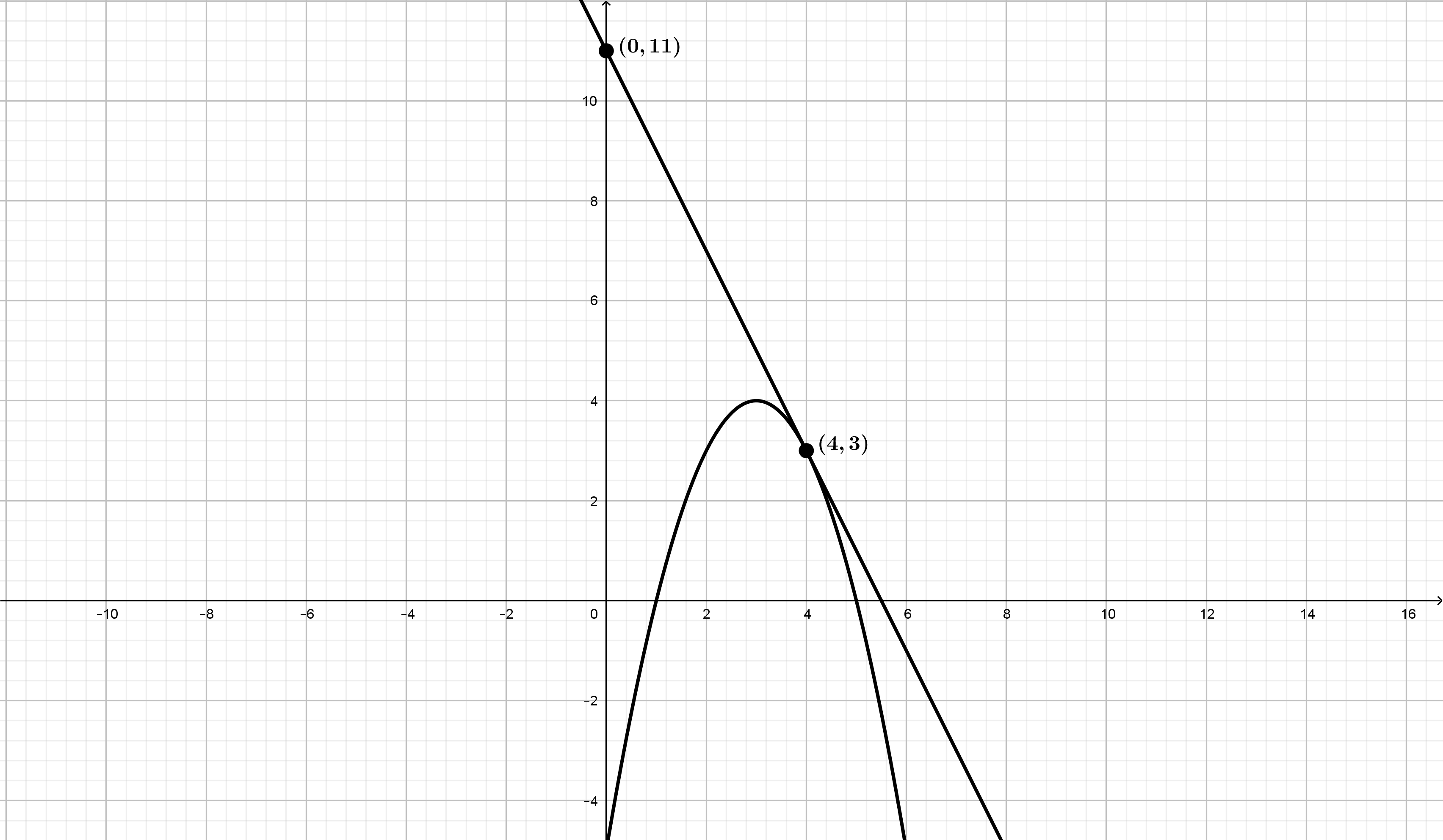
Se considera la función \(f(x)=-x^2+6x+c\)
- Calcule el valor del parámetro \(c\) para que la recta tangente a la gráfica de la función en el punto de abscisa \(x=4\) pase por el punto \((0,11)\).
- Calcule el área de la región acotada limitada por las gráficas de \(f(x)=-x^2+6x-5\) y \(g(x)=5-x\).
-
La ecuación de la recta tangente a la función \(f(x)=-x^2+6x+c\) en el punto de abscisa \(x=4\) es de la forma:
$$y-f(4)=f'(4)(x-4)$$
$$
\left\{\begin{array}{l}
f(4)=-4^2+6 \cdot 4+c=-16+24+c=c+8\\
f'(x)=-2x+6 \Rightarrow f'(4)=-2 \cdot 4+6=-2\\
\end{array}\right.
$$
Sustituyendo en la ecuación de la recta tangente se obtiene que:
\(y-(c+8)=-2(x-4) \Rightarrow y-c-8=-2x+8 \Rightarrow y=-2x+16+c\)
Como la recta tangente a la gráfica de la función pasa por el punto \((0,11)\), sustituyendo se obtiene que:
\(11=-2 \cdot 0+16+c \Rightarrow c=-5\)
Por tanto, \(f(x)=-x^2+6x-5\) y la recta tangente es \(y=-2x+11\)
 -
Resolviendo la ecuación \(f(x)=g(x)\) se obtiene que \(-x^2+6x-5=5-x \Rightarrow x^2-7x+10=0 \Rightarrow
\left\{\begin{array}{c}
x=2\\
ó\\
x=5\\
\end{array}\right.\)
\(Área(\mathbf{R})=\displaystyle{\int_{2}^{5}{\left(f(x)-g(x)\right)dx}}=\displaystyle{\int_{2}^{5}{\left((-x^2+6x-5)-(5-x)\right)dx}}=\displaystyle{\int_{2}^{5}{\left(-x^2+7x-10\right)dx}}\)
Calculamos la integral indefinida:
\(F(x)=\displaystyle{\int{\left(-x^2+7x-10\right)dx}}=\displaystyle{-\int{x^2dx}}+\displaystyle{7\int{xdx}}-\displaystyle{10\int{1dx}}=\displaystyle{-\frac{x^3}{3}}+\displaystyle{\frac{7x^2}{2}}-10x+C\)
Y aplicando la regla de Barrow:
\(\displaystyle{\int_{2}^{5}{\left(-x^2+7x-10\right)dx}}=\left[F(x)\right]_{x=2}^{x=5}=\left[\displaystyle{-\frac{x^3}{3}}+\displaystyle{\frac{7x^2}{2}}-10x+C\right]_{x=2}^{x=5}=\)
\(=\left(\displaystyle{-\frac{5^3}{3}}+\displaystyle{\frac{7 \cdot 5^2}{2}}-10 \cdot 5+C\right)-\left(\displaystyle{-\frac{2^3}{3}}+\displaystyle{\frac{7 \cdot 2^2}{2}}-10 \cdot 2+C\right)=\)
\(=\displaystyle{-\frac{125}{3}}+\displaystyle{\frac{175}{2}}-50+C+\displaystyle{\frac{8}{3}}-\displaystyle{\frac{28}{2}}-20-C=\displaystyle{\frac{9}{2}}\)
Por tanto, el \(Área(\mathbf{R})=\displaystyle{\frac{9}{2}}\)
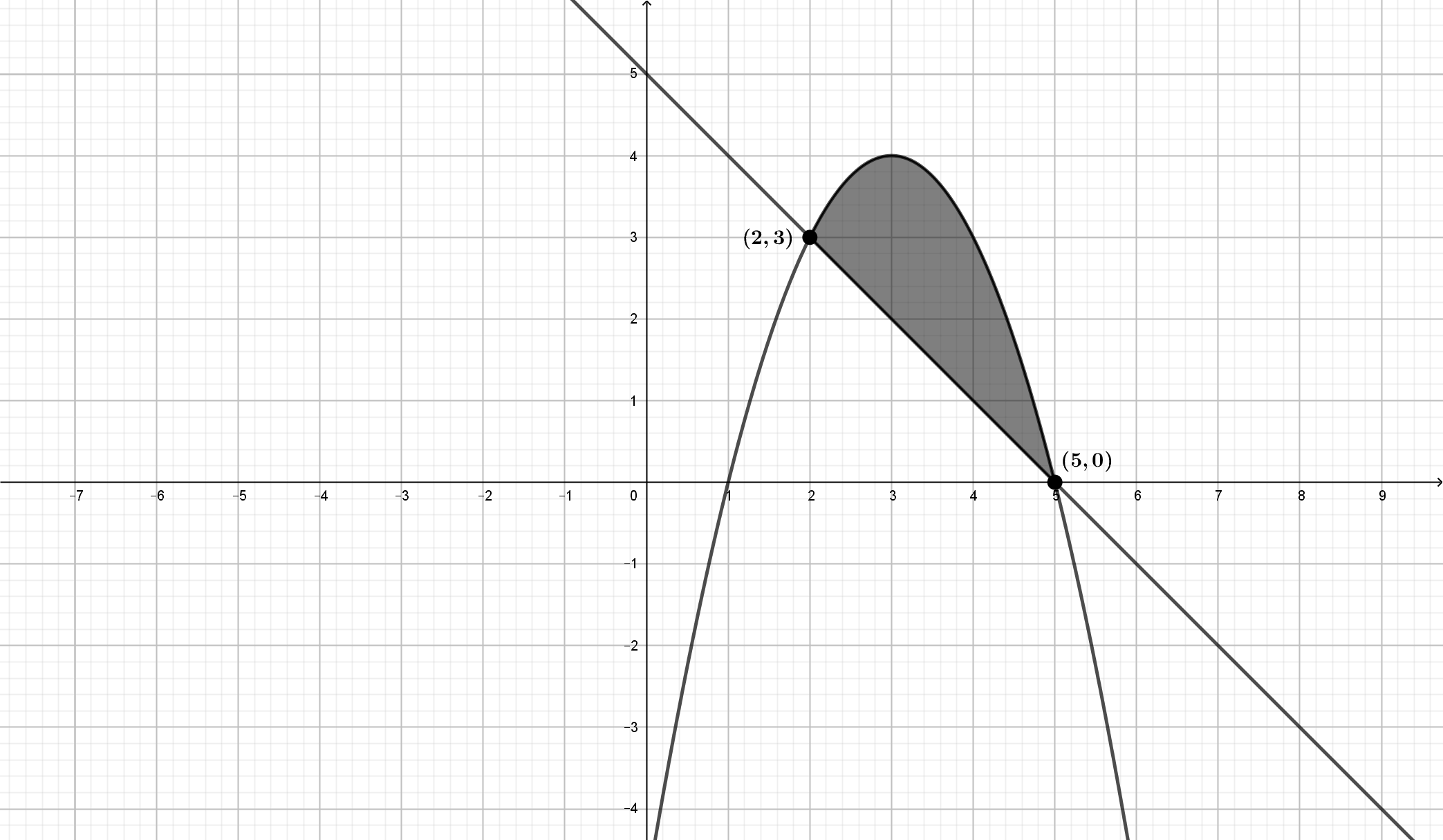
|
Problema (#2)
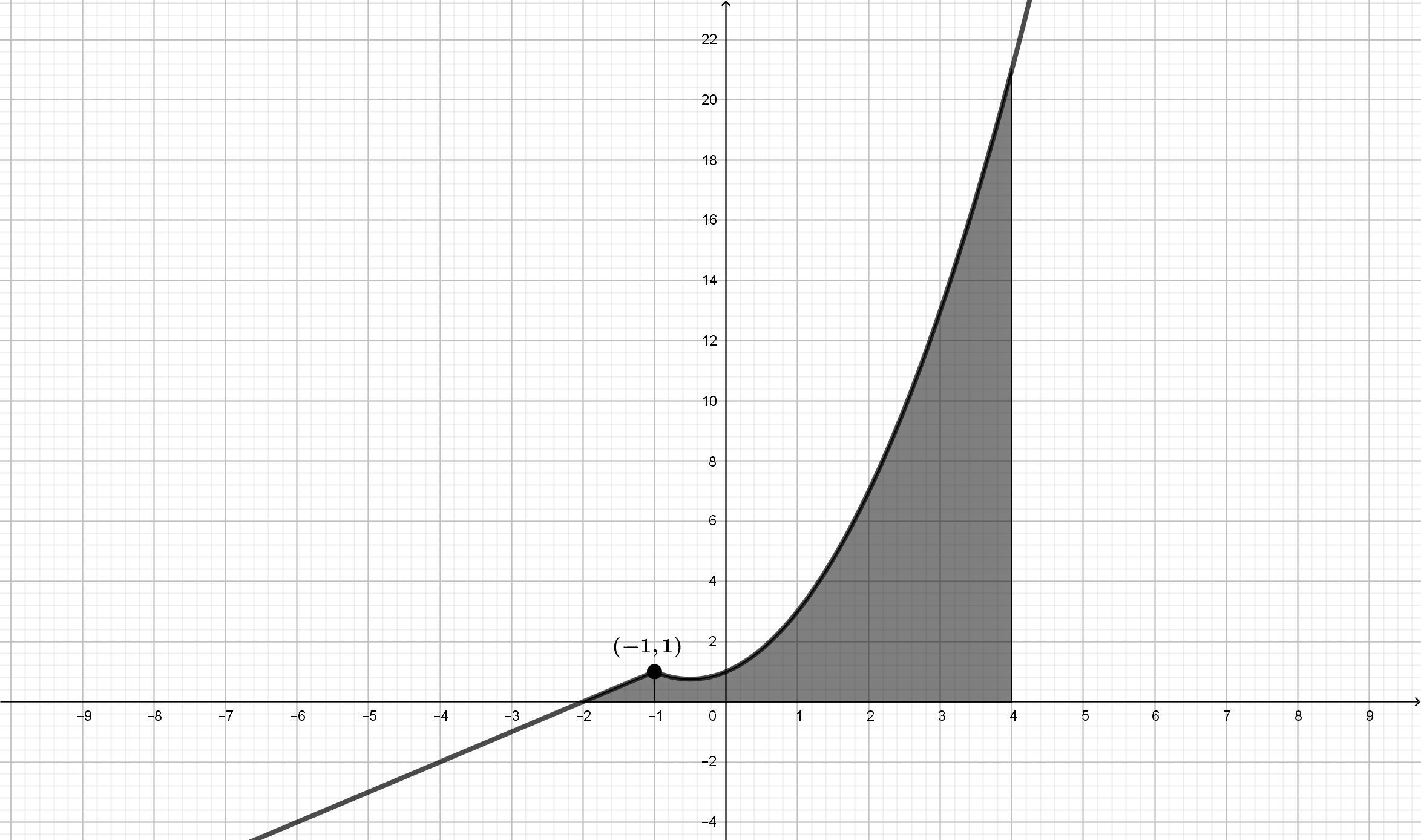
Se considera la función dada por \(f(x)= \left\{\begin{array}{lcc}
x+2 & si & x < -1\\
x^2+x+1 & si & x \geq -1\\
\end{array}\right.\)
- Estudie la derivabilidad de la función \(f\).
- Calcule \(\displaystyle{\int_{-2}^{4}f(x) dx}\)
-
Continuidad:
\(f(x)\) es continua en \(\mathbb{R}-\{-1\}\), al ser una función a trozos y ambos trozos son polinomios.
Continuidad en \(x=-1\)
\(\left. \begin{array}{l}
1) f(-1)=(-1)^2+(-1)+1=1\\
2) \displaystyle\lim_{x \rightarrow -1} f(x)=
\left \{ \begin{array}{l}
\displaystyle\lim_{x \rightarrow -1^{-}} x+2=-1+2=+1\\
\displaystyle\lim_{x \rightarrow -1^{+}} x^2+x+1=(-1)^2+(-1)+1=1\\
\end{array}
\right.\\
\end{array}
\right\} \Rightarrow f(x)\) continua en \(x=-1\)
Derivabilidad:
\(f'(x)= \left\{\begin{array}{lcc}
1 & si & x < -1\\
2x+1 & si & x > -1\\
\end{array}\right.\)
Derivabilidad en \(x=-1\)
\(\left. \begin{array}{l}
f'(1^{-})=\displaystyle\lim_{x \rightarrow -1^{-}} 1=1\\
f'(1^{+})=\displaystyle\lim_{x \rightarrow -1^{+}} 2x+1=2(-1)+1=-1\\
\end{array}
\right\} \Rightarrow f(x)\) no es derivable en \(x=-1\)
-
\(\displaystyle{\int_{-2}^{4}{f(x)dx}}=\displaystyle{\int_{-2}^{-1}{f(x)dx}}+\displaystyle{\int_{-1}^{4}{f(x)dx}}=\displaystyle{\int_{-2}^{-1}{\left(x+2\right)dx}}+\displaystyle{\int_{-1}^{4}{\left(x^2+x+1\right)dx}}\)
Calculamos las integrales indefinidas:
\(F_{1}(x)=\displaystyle{\int{\left(x+2\right)dx}}=\displaystyle{\frac{x^2}{2}}+2x+C_1\)
\(F_{2}(x)=\displaystyle{\int{\left(x^2+x+1\right)dx}}=\displaystyle{\frac{x^3}{3}}+\displaystyle{\frac{x^2}{2}}+x+C_2\)
Aplicamos la regla de Barrow:
\(\displaystyle{\int_{-2}^{4}{f(x)dx}}=\left[F_{1}(x)\right]_{x=-2}^{x=-1}+\left[F_{2}(x)\right]_{x=-1}^{x=4}=\left(\left(\displaystyle{\frac{(-1)^2}{2}}+2(-1)+C_1\right)-\left(\displaystyle{\frac{(-2)^2}{2}}+2(-2)+C_1\right)\right)+\)
\(+\left(\left(\displaystyle{\frac{4^3}{3}}+\displaystyle{\frac{4^2}{2}}+4+C_2\right)-\left(\displaystyle{\frac{(-1)^3}{3}}+\displaystyle{\frac{(-1)^2}{2}}+(-1)+C_2\right)\right)=\displaystyle{\frac{1}{2}}+\displaystyle{\frac{205}{6}}=\displaystyle{\frac{104}{3}}\)
|
Problema (#3)
Se considera la función dada por \(f(x)= \left\{\begin{array}{lcc}
\displaystyle{\frac{2x}{x-1}} & si & x < 0\\
-2x^2+3x+2 & si & x \geq 0\\
\end{array}\right.\)
- Estudie la continuidad y la derivabilidad de la función \(f\).
- Analice la monotonía y determine los extremos relativos de \(f\).
- Calcule el área de la región limitada por la gráfica de \(f\) y el eje \(\hbox{OX}\) en el intervalo \([0,2]\).
-
Continuidad:
\(f(x)=\displaystyle{\frac{2x}{x-1}}\) es continua en \(\mathbb{R}-\{1\}\), al ser racional, en particular si \(x < 0\).
\(f(x)=-2x^2+3x+2\) es continua en \(\mathbb{R}\), al ser un polinomio, en particular si \(x > 0\).
Continuidad en \(x=0\)
\(\left. \begin{array}{l}
1) f(0)=-2 \cdot 0^2+3 \cdot 0+2=2\\
2) \displaystyle\lim_{x \rightarrow 0} f(x)=
\left \{ \begin{array}{l}
\displaystyle\lim_{x \rightarrow 0^{-}} \displaystyle{\frac{2x}{x-1}}=\displaystyle{\frac{2 \cdot 0}{0-1}}=0\\
\displaystyle\lim_{x \rightarrow 0^{+}} -2x^2+3x+2=-2 \cdot 0^2+3 \cdot 0+2=2\\
\end{array}
\right.\\
\end{array}
\right\} \Rightarrow f(x)\) no es continua en \(x=0\)
Derivabilidad:
\(f'(x)= \left\{\begin{array}{lcc}
\displaystyle{\frac{-2}{(x-1)^2}} & si & x < 0\\
-4x+3 & si & x > 0\\
\end{array}\right.\)
Derivabilidad en \(x=0\)
\(f(x)\) no es derivable en \(x=0\), puesto que \(f(x)\) no es continua en \(x=0\).
-
Monotonía y extremos:
Igualamos la derivada primera a cero y resolvemos la ecuación:
\(f'(x)=0 \Leftrightarrow \left\{\begin{array}{lcc}
\displaystyle{\frac{-2}{(x-1)^2}}=0 & si & x < 0\\
-4x+3=0 & si & x > 0\\
\end{array}\right.
\Leftrightarrow \left\{\begin{array}{lcc}
-2=0 & si & x < 0\\
\displaystyle{x=\frac{3}{4}} & si & x > 0\\
\end{array}\right.\)
Estudiamos el signo de \(f'(x)\):
\(\left. \begin{array}{l}
f'(x) < 0 \hbox{ en } (-\infty,0) \cup \displaystyle{\left(\displaystyle{\frac{3}{4}},+\infty\right)}\\
f'(x) =0 \hbox{ si } x=\displaystyle{\frac{3}{4}} \\
f'(x) > 0 \hbox{ en } \displaystyle{\left(0,\displaystyle{\frac{3}{4}}\right)}\\
\end{array}
\right\}
\Rightarrow
\left. \begin{array}{l}
f \searrow \hbox{ en } (-\infty,0) \cup \displaystyle{\left(\displaystyle{\frac{3}{4}},+\infty\right)}\\
f \nearrow \hbox{ en } \displaystyle{\left(0,\displaystyle{\frac{3}{4}}\right)}\\
\end{array}
\right\}
\Rightarrow
\left.
\begin{array}{l}
f(x) \hbox{ tiene un máximo relativo en } x=\displaystyle{\frac{3}{4}}\\
\end{array}
\right.\)
-
\(\displaystyle{\int_{0}^{2}{f(x)dx}}=\displaystyle{\int_{0}^{2}{\left(-2x^2+3x+2\right)dx}}\)
Calculamos la integral indefinida:
\(F(x)=\displaystyle{\int{\left(-2x^2+3x+2\right)dx}}=\displaystyle{\frac{-2x^3}{3}+\frac{3x^2}{2}+2x+C}\)
Aplicamos la regla de Barrow:
\(\displaystyle{\int_{0}^{2}{f(x)dx}}=\left[F(x)\right]_{x=0}^{x=2}=\left(\displaystyle{\frac{-2 \cdot 2^3}{3}+\frac{3 \cdot 2^2}{2}+2 \cdot 2+C}\right)-\left(\displaystyle{\frac{-2 \cdot 0^3}{3}+\frac{3 \cdot 0^2}{2}+2 \cdot 0+C}\right)=\)
\(=\displaystyle{\frac{-16}{3}+6+4+C}-C=\displaystyle{\frac{14}{3}}\)

|
Problema (#4)
Dadas las funciones \(f(x)=-x^2+3x+2\) y \(g(x)=2x^2-6x-10\),
- Calcule los puntos de corte de las gráficas de \(f\) y \(g\).
- Calcule el área de la región acotada delimitada por las dos gráficas.
-
Resolviendo la ecuación \(f(x)=g(x)\) se obtiene que \(-x^2+3x+2=2x^2-6x-10 \Rightarrow x^2-3x-4=0 \Rightarrow
\left\{\begin{array}{c}
x_1=-1\\
ó\\
x_2=4\\
\end{array}\right.\)
Sustituyendo los valores obtenidos para \(x\) en la ecuación de \(f(x)\) o \(g(x)\), obtenemos los de \(y\):
Si \(\left\{\begin{array}{l}
x_1=-1 \Rightarrow y_1=-2\\
x_2=4 \Rightarrow y_2=-2\\
\end{array}\right.
\Rightarrow\)
Los puntos de corte de ambas gráficas son
\(\left\{\begin{array}{l}
A(-1,-2)\\
B(4,-2)\\
\end{array}\right.\)
-
\(Área(\mathbf{R})=\displaystyle{\int_{-1}^{4}{\left(f(x)-g(x)\right)dx}}=\displaystyle{\int_{-1}^{4}{\left((-x^2+3x+2)-(2x^2-6x-10)\right)dx}}=\displaystyle{\int_{-1}^{4}{\left(-3x^2+9x+12\right)dx}}\)
Calculamos la integral indefinida:
\(F(x)=\displaystyle{\int{\left(-3x^2+9x+12\right)dx}}=\displaystyle{-\int{3x^2dx}}+\displaystyle{9\int{xdx}}+\displaystyle{12\int{1dx}}=\displaystyle{-x^3}+\displaystyle{\frac{9x^2}{2}}+12x+C\)
Y aplicando la regla de Barrow:
\(\displaystyle{\int_{-1}^{4}{\left(-3x^2+9x+12\right)dx}}=\left[F(x)\right]_{x=-1}^{x=4}=\left[\displaystyle{-x^3}+\displaystyle{\frac{9x^2}{2}}+12x+C\right]_{x=-1}^{x=4}=\)
\(=\left(\displaystyle{-4^3}+\displaystyle{\frac{9 \cdot 4^2}{2}}+12 \cdot 4+C\right)-\left(\displaystyle{-(-1)^3}+\displaystyle{\frac{9(-1)^2}{2}}+12(-1)+C\right)=\)
\(=-64+72+48+C-1-\displaystyle{\frac{9}{2}}+12-C=\displaystyle{\frac{125}{2}}\)
Por tanto, el \(Área(\mathbf{R})=\displaystyle{\frac{125}{2}}\)

|
Problema (#5)
Se considera la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) definida por \(f(x)= \left\{\begin{array}{lcc}
-x^2+x+a & si & x \leq 1\\
\displaystyle{\frac{b}{x+1}} & si & x > 1\\
\end{array}\right.\)
- Determine \(a\) y \(b\) para que \(f\) sea continua y derivable en \(\mathbb{R}\).
- Para \(a=2\) y \(b=4\), represente gráficamnte \(f\).
- Para \(a=2\) y \(b=4\), calcule el área del recinto limitado por la gráfica de \(f\), el eje \(\hbox{OX}\) y las rectas \(x=0\) y \(x=1\).
-
Continuidad:
\(f(x)=-x^2+x+a\) es continua en \(\mathbb{R}\), al ser un polinomio, en particular si \(x < 1\).
\(f(x)=\displaystyle{\frac{b}{x+1}}\) es continua en \(\mathbb{R}-\{-1\}\), al ser racional, en particular si \(x > 1\).
Continuidad en \(x=1\)
\(\left. \begin{array}{l}
1) f(1)=-1^2+1+a=-1+1+a=a\\
2) \displaystyle\lim_{x \rightarrow 1} f(x)=
\left \{ \begin{array}{l}
\displaystyle\lim_{x \rightarrow 1^{-}} -x^2+x+a=-1^2+1+a=-1+1+a=a\\
\displaystyle\lim_{x \rightarrow 1^{+}} \displaystyle{\frac{b}{x+1}}=\displaystyle{\frac{b}{1+1}}=\displaystyle{\frac{b}{2}}\\
\end{array}
\right.\\
\end{array}
\right\} \Rightarrow f(x)\) es continua en \(x=1\) si \(a=\displaystyle{\frac{b}{2}} \Leftrightarrow 2a-b=0\) (*)
Derivabilidad:
\(f'(x)= \left\{\begin{array}{lcc}
-2x+1 & si & x < 1\\
\displaystyle{\frac{-b}{(x+1)^2}} & si & x > 1\\
\end{array}\right.\)
Derivabilidad en \(x=1\)
\(\left. \begin{array}{l}
f'(1^{-})=\displaystyle\lim_{x \rightarrow -1^{-}} -2x+1=-2 \cdot 1+1=-1\\
f'(1^{+})=\displaystyle\lim_{x \rightarrow -1^{+}} \displaystyle{\frac{-b}{(x+1)^2}}=\displaystyle{\frac{-b}{(1+1)^2}}=\displaystyle{\frac{-b}{2^2}}=\displaystyle{\frac{-b}{4}}\\
\end{array}
\right\} \Rightarrow f(x)\) es derivable en \(x=1\) si \(-1=\displaystyle{\frac{-b}{4}} \Leftrightarrow b=4\) (**)
Sustituyendo el valor de \(b\) en (*) se obtiene que \(2a-4=0\ \Rightarrow a=2\)
Por tanto, \(f(x)\) es derivable en \(\mathbb{R}\) si \(a=2\) y \(b=4\).
-
Para representar la función \(f(x)= \left\{\begin{array}{lcc}
-x^2+x+2 & si & x \leq 1\\
\displaystyle{\frac{4}{x+1}} & si & x > 1\\
\end{array}\right.\), dibujamos cada trozo en su correspondiente dominio de definición:
\(f(x)=-x^2+x+2\) es una parábola. Su vértice es el punto \(\displaystyle{V\left(\frac{1}{2},\frac{9}{4}\right)}\)
Puntos de corte con los ejes:
Eje X (y=0): \(0=-x^2+x+2 \Leftrightarrow
\left\{\begin{array}{c}
x=-1\\
ó\\
x=2\\
\end{array}\right.\Rightarrow
\left\{\begin{array}{c}
A(-1,0)\\
B(2,0)\\
\end{array}\right.
\)
Eje Y (x=0): \(y=-0^2+0+2 \Leftrightarrow y=2 \Rightarrow C(0,2)\)
Tabla de valores:
| \(x\) |
\(-2\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
| \(y\) |
\(-4\) |
\(0\) |
\(2\) |
\(\displaystyle{\frac{9}{2}}\) |
\(2\) |
\(f(x)=\displaystyle{\frac{4}{x+1}}\) es una hipérbola.
Asíntotas: Horizontal en \(y=0\) y Vertical en \(x=0\)
Tabla de valores:
| \(x\) |
\(1\) |
\(2\) |
\(4\) |
\(8\) |
| \(y\) |
\(2\) |
\(\displaystyle{\frac{4}{3}}\) |
\(\displaystyle{\frac{4}{5}}\) |
\(\displaystyle{\frac{4}{9}}\) |
-
\(\displaystyle{\int_{0}^{1}{f(x)dx}}=\displaystyle{\int_{0}^{1}{\left(-x^2+x+2\right)dx}}\)
Calculamos la integral indefinida:
\(F(x)=\displaystyle{\int{\left(-x^2+x+2\right)dx}}=\displaystyle{\frac{-x^3}{3}+\frac{x^2}{2}+2x+C}\)
Aplicamos la regla de Barrow:
\(\displaystyle{\int_{0}^{1}{f(x)dx}}=\left[F(x)\right]_{x=0}^{x=1}=\left(\displaystyle{\frac{-1^3}{3}+\frac{1^2}{2}+2 \cdot 1+C}\right)-\left(\displaystyle{\frac{-0^3}{3}+\frac{0^2}{2}+2 \cdot 0+C}\right)=\)
\(=\displaystyle{\frac{-1}{3}+\frac{1}{2}+2+C}-C=\displaystyle{\frac{13}{6}}\)
|
Problema (#6)
Se consideran las funciones \(f\) y \(g\), definidas en \(\mathbb{R}\) de la siguiente forma: \(f(x)=x^2\) y \(g(x)=4-x^2\)
- Calcule los puntos de corte de las gráficas de \(f\) y \(g\).
- Represente sobre un mismo sistema de coordenadas cartesianas las gráficas de \(f\) y \(g\) y calcule el área de la región del plano delimitada por las gráficas de ambas funciones.
|
Problema (#7)
Se considera la función \(f(x)= \left\{\begin{array}{lcc}
x+a & si & x < 1\\
x^2-2 & si & 1 \leq x \leq 3\\
x+b & si & x \geq 3\\
\end{array}\right.\)
- Determine los valores de \(a\) y \(b\) para que la función sea continua en \(\mathbb{R}\).
- Para \(a=-2\) y \(b=4\), calcule \(\displaystyle{\int_{0}^{5} f(x) dx}\).
|
Problema (#8)
Se considera la función \(f(x)= \left\{\begin{array}{lcc}
2x^3-2x^2+4 & si & x \leq 1\\
x^2+3 & si & x > 1\\
\end{array}\right.\)
- Estudie la continuidad y derivabilidad de \(f\).
- Calcule el máximo y el mínimo de \(f\) en el intervalo \([-1,1]\).
- Calcule el área de la región limitada por la gráfica de \(f\) y el eje abscisas en el intervalo \([0,2]\).
|
Problema (#9)
Se considera la función \(f(x)= \left\{\begin{array}{lcc}
\displaystyle{\frac{-3}{x+1}} & si & x < 0\\
-x^2+4x & si & x \geq 0\\
\end{array}\right.\)
- Estudie la continuidad y derivabilidad de \(f\).
- Estudie la monotonía y calcule la abscisa de los extremos relativos.
- Calcule el área de la región limitada por la gráfica de \(g(x)=-x^2+4x\) y el eje \(\hbox{OX}\).
|
Problema (#10)
Se considera la función \(f(x)= \left\{\begin{array}{lcc}
2x-x^2-3 & si & x < 0\\
\displaystyle{\frac{3}{x-1}} & si & x \geq 0\\
\end{array}\right.\)
- Compruebe que \(f\) es continua en \(x=0\). ¿Es derivable en \(x=0\)?
- Calcule el área de la región limitada por la gráfica de \(f(x)\), las rectas \(x=-1\), \(x=\displaystyle{\frac{1}{2}}\) y el eje \(\hbox{OX}\).
|
Problema (#11)
Una empresa conoce que el gasto instantáneo de combustible que le genera una de sus máquinas viene dado por la expresión \(f(x)=x(x-5)(x-7), x \in [0,5]\), donde \(x\) viene dado en horas.
- Calcule para qué valor de \(x\) se tiene que \(f\) alcanza un valor máximo.
- Calcule el gasto total de combustible consumido.
-
Si el gasto instantáneo de combustible viene dado por la expresión \(f(x)=x(x-5)(x-7), x \in [0,5]\), donde \(x\) viene dado en horas, para calcular el valor máximo, derivamos y estudiamos el signo de su derivada.
\(f(x)=x(x-5)(x-7)=x^3-12x^2+35x, x \in [0,5]\)
\(f'(x)=\left(x^3-12x^2+35x\right)'=3x^2-24x+35, x \in [0,5]\)
Igualamos la derivada primera a cero y resolvemos la ecuación:
\(f'(x)=0 \Leftrightarrow 3x^2-24x+35=0 \Leftrightarrow
\left\{\begin{array}{cl}
x_1=4-\displaystyle{{\frac{\sqrt[]{39}}{3}}} & (0 \leq x_1 \leq 5)\\
ó\\
x_2=4+\displaystyle{{\frac{\sqrt[]{39}}{3}}} & (x_2 > 5)\\
\end{array}\right.\)
Estudiamos el signo de \(f′(x)\):
\(\left. \begin{array}{l}
f'(x) > 0 \hbox{ en } \displaystyle{\left(0,4-\displaystyle{{\frac{\sqrt[]{39}}{3}}}\right)}\\
f'(x) =0 \hbox{ si } x=4-\displaystyle{{\frac{\sqrt[]{39}}{3}}}\\
f'(x) < 0 \hbox{ en } \displaystyle{\left(4-\displaystyle{{\frac{\sqrt[]{39}}{3}}},5\right)}\\
\end{array}
\right\}
\Rightarrow
\left. \begin{array}{l}
f \nearrow \hbox{ en } \displaystyle{\left(0,4-\displaystyle{{\frac{\sqrt[]{39}}{3}}}\right)}\\
f \searrow \hbox{ en } \displaystyle{\left(4-\displaystyle{{\frac{\sqrt[]{39}}{3}}},5\right)}\\
\end{array}
\right\}
\Rightarrow
\left.
\begin{array}{l}
f(x) \hbox{ tiene un máximo relativo en } x=4-\displaystyle{{\frac{\sqrt[]{39}}{3}}}\\
\end{array}
\right.\)
-
Como el gasto instantáneo en combustible es una función positiva en \([0,5]\), el gasto total de combustible consumido se calcula mediante:
\(\displaystyle{\int_{0}^{5}{x(x-5)(x-7)dx}}=\displaystyle{\int_{0}^{5}{\left(x^3-12x^2+35x\right)dx}}\)
Calculamos la integral indefinida:
\(F(x)=\displaystyle{\int{\left(x^3-12x^2+35x\right)dx}}=\displaystyle{\frac{x^4}{4}-\frac{12x^3}{3}+\frac{35x^2}{2}+C}=\displaystyle{\frac{x^4}{4}-4x^3+\frac{35x^2}{2}+C}\)
Aplicamos la regla de Barrow:
\(\displaystyle{\int_{0}^{5}{f(x)dx}}=\left[F(x)\right]_{x=0}^{x=5}=\left(\displaystyle{\frac{5^4}{4}-4 \cdot 5^3+\frac{35 \cdot 5^2}{2}+C}\right)-\left(\displaystyle{\frac{0^4}{4}-4 \cdot 0^3+\frac{35 \cdot 0^2}{2}+C}\right)=\)
\(=\displaystyle{\frac{625}{4}-500+\frac{875}{2}}+C-C=\displaystyle{\frac{375}{4}}\)
|
Problema (#12)
Dadas las funciones \(f(x)=x^2-8x+16\) y \(g(x)=x-2\), se pide:
- Represente ambas funciones en los mismos ejes coordenados.
- Determine los puntos de corte entre las gráficas de ambas funciones.
- Calcule el área delimitada por las gráficas de ambas funciones.
|
Problema (#13)
De la función \(C(q)\) que representa los costes de producción de una empresa, en miles de euros, en función de la cantidad fabricada \(q\), en miles de kilogramos, se sabe que su derivada viene dada por la función \(C'(q)=60q^2-80q+35\). Se pide:
- Obtenga los intervalos de crecimiento y decrecimiento de la función \(C(q)\) y esboce la gráfica de la función \(C'(q)\) en el intervalo \((0,15)\).
- Obtenga los intervalos de concavidad y convexidad de la función de costes \(C(q)\).
- ¿Cuál es el coste adicional que debe asumir la empresa si decide pasar de fabricar \(1000 Kg\) a fabricar \(1500 Kg\)?
-
Monotonía y extremos:
Igualamos la derivada primera a cero y resolvemos la ecuación:
\(C'(q)=0 \Leftrightarrow 60q^2-80q+35=0.\) Se observa al resolverla que no tiene soluciones reales.
Estudiamos el signo de \(C'(q)\):
Como la ecuación \(C'(q)=0\) no tiene soluciones en \(\mathbb{R}\), entonces \(C'(q)\) nunca es \(0\), por tanto, siempre será positiva o negativa.
\(C'(q) > 0\) en \(\displaystyle{\left(0,15\right)} \Rightarrow C(q) \nearrow \hbox{ en } \displaystyle{\left(0,15\right)}\)
\(C'(q)=60q^2-80q+35\) es una parábola. Su vértice es el punto \(\displaystyle{V\left(\frac{2}{3},\frac{25}{3}\right)}\)
Puntos de corte con los ejes:
Eje X (C'(q)=0): \(0=60q^2-80q+35\) No tiene soluciones reales
Eje Y (q=0): \(y=60 \cdot 0^2-80 \cdot 0+35 \Leftrightarrow y=35 \Rightarrow C(0,35)\)
Tabla de valores:
| \(q\) |
\(0\) |
\(\displaystyle{\frac{2}{3}}\) |
\(1.5\) |
| \(C'(q)\) |
\(35\) |
\(\displaystyle{\frac{25}{3}}\) |
\(50\) |
-
Concavidad y convexidad. Puntos de inflexión:
\(C''(q)=120q-80\)
Igualamos la derivada segunda a cero y resolvemos la ecuación:
\(C''(q)=0 \Leftrightarrow 120q-80=0 \Leftrightarrow q=\displaystyle{\frac{2}{3}}\)
Estudiamos el signo de \(C''(q)\):
\(\left. \begin{array}{l}
C''(q) < 0 \hbox{ en } \displaystyle{\left(0,\displaystyle{\frac{2}{3}}\right)}\\
C''(q) =0 \hbox{ si } x=\displaystyle{\frac{2}{3}}\\
C''(q) > 0 \hbox{ en } \displaystyle{\left(\displaystyle{\frac{2}{3}},5\right)}\\
\end{array}
\right\}
\Rightarrow
\left. \begin{array}{l}
C(q) \hbox{ es cóncava en } \displaystyle{\left(0,\displaystyle{\frac{2}{3}}\right)}\\
C(q) \hbox{ es convexa en } \displaystyle{\left(\displaystyle{\frac{2}{3}},5\right)}\\
\end{array}
\right\}
\Rightarrow
\left.
\begin{array}{l}
f(x) \hbox{ tiene un punto de inflexión en } x=\displaystyle{\frac{2}{3}}\\
\end{array}
\right.\)
-
Aplicando la linealidad de la integral:
\(C(q)=\displaystyle{\int{C'(q)dq}}=\displaystyle{\int{\left(60q^2-80q+35\right)dq}}=\displaystyle{60\int{q^2dq}}-\displaystyle{80\int{qdq}}+\displaystyle{35\int{1dq}}=\)
\(=\displaystyle{\frac{60q^3}{3}}-\displaystyle{\frac{80q^2}{2}}+\displaystyle{35q}+K=20q^3-40q^2+35q+K\)
El coste adicional que debe asumir la empresa si decide pasar de fabricar \(1000 Kg\) a fabricar \(1500 Kg\) será la diferencia entre ambos costes de producción:
Como la cantidad fabricada \(q\) se expresa en miles de Kilogramos, entonces \(1000 Kg \equiv 1\) y \(1500 Kg \equiv 1.5\).
\(C(1.5)-C(1)=\displaystyle{\left(20 \cdot 1.5^3-40 \cdot 1.5^2+35 \cdot 1.5+K\right)}-\displaystyle{\left(20 \cdot 1^3-40 \cdot 1^2+35 \cdot 1+K\right)}=\)
\(=\displaystyle{\left(30+K\right)}-\displaystyle{\left(15+K\right)}=30+K-15-K=15\)
Por tanto, el coste adicional que debe asumir la empresa es de \(15000\) €.
|
Problema (#14)
La temperatura en el interior de un horno de cerámica viene dada por la función \(f(t)=-t^2+4t+5, t \in [0,5]\), donde \(t\) representa el tiempo en horas y \(f(t)\) está expresado en cientos de ºC.
- Estudie la monotonía de \(f\) y calcule la temperatura máxima alcanzada.
- Represente gráficamente \(f(t)\).
- Calcule \(\displaystyle{\int_{0}^{5} f(t) dt}\).
|
Problema (#15)
Dada la función \(f(x)=x^3-4x^2+4x\),
- Estudie su monotonía y calcule sus extremos.
- Represente gráficamente la función.
- Obtenga su primitiva.
- Calcule el área de la región acotada limitada por la gráfica de \(f\) y el eje de abscisas entre \(x=0\) y \(x=2\).
|
Problema (#16)
La función que mide la concentración plasmática de un fármaco en función del tiempo, medida en \(mg/l\), viene dada por la expresión \(C(t)= \left\{\begin{array}{lcc}
-t^2+4.5t & si & 0 \leq t \leq 4\\
\displaystyle{\frac{4}{t-2}} & si & t \geq 4\\
\end{array}\right.\), donde \(t\) es el tiempo transcurrido, en horas, despuésde administrar el fármaco.
- Estudie la continuidad de la función \(C(t)\).
- ¿En qué momento se detecta la concentración máxima del fármaco en la sangre y cuál es dicha concentración?
- Esboce la gráfica de \(C(t)\).
- Calcule el área bajo la curva \(C(t)\) entre las \(0\) horas y las \(6\) horas.
|
Problema (#17)
Se considera la función dada por \(f(x)= \left\{\begin{array}{lcc}
x+2 & si & x < -1\\
x^2+x+1 & si & x \geq -1\\
\end{array}\right.\)
- Estudie la monotonía de la función \(f\).
- Calcule el área de la figura limitada por la gráfica de \(f\), el eje de abscisas y las rectas \(x=0\) y \(x=2\).
|
Problema (#18)
Se considera la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) definida por \(f(x)= \left\{\begin{array}{lcc}
-5x-10 & si & x \leq -1\\
-x^2+2x-2 & si & x > -1\\
\end{array}\right.\)
- Esboce la gráfica de \(f\).
- Calcule el área de la región limitada por la gráfica de \(f(x)\), el eje de abscisas y la recta \(x=2\).
|
Problema (#19)
Dadas la parábola \(f(x)=3x^2\) y la recta \(g(x)=-3x+6\), se pide:
- Represente sobre un mismo sistema de coordenadas cartesianas la gráfica de cada función.
- Calcule el área del recinto plano limitado por las gráficas de \(f\) y \(g\).
|
Problema (#20)
Calcula el área limitada por las gráficas de la función \(f(x)=x^3-3x\) y de la recta \(y=x\).
|
Algunos resultados teóricos
Integrales:
Integral indefinida. Integrales inmediatas
Dada una función \(f(x)\) continua, se define una primitiva (o integral) de \(f(x)\), como una función \(F(x)\) tal que \(F'(x)=f(x)\).
En ese caso, decimos que \(F(x)=\displaystyle{\int{f(x) dx}} + C\), donde \( C \in \mathbb{R} \) (Notación de Leibnitz)
$$
\left\{\begin{array}{l}
\displaystyle{\int{k dx}} = kx + C\\
\displaystyle{\int{x^{n} dx}} = \displaystyle{\frac{x^{n+1}}{n+1}} + C, (n \neq -1)\\
\displaystyle{\int{\frac{1}{x} dx}} = Ln|x| + C\\
\displaystyle{\int{e^{x} dx}} = e^{x} + C\\
\displaystyle{\int{a^{x} dx}} = \displaystyle{\frac{a^{x}}{Ln|a|}} + C\\
\displaystyle{\int{cos(x) dx}} = sen(x) + C\\
\displaystyle{\int{sen(x) dx}} = -cos(x) + C\\
\displaystyle{\int{\left(1+tg^2(x)\right) dx}} = \displaystyle{\int{\frac{1}{cos^2(x)} dx}} = tg(x) + C\\
\displaystyle{\int{\left(1+cotg^2(x)\right) dx}} = \displaystyle{\int{\frac{1}{sen^2(x)} dx}} = -cotg(x) + C\\
\displaystyle{\int{\frac{1}{\sqrt[]{1-x^2}} dx}} = arcsen(x) + C\\
\displaystyle{\int{\frac{1}{1+x^2} dx}} = arctg(x) + C\\
\end{array}\right.
$$
Métodos de Integración: Integral de formas compuestas (Cambio de variable)
$$
\left\{\begin{array}{l}
\displaystyle{\int{u'(x) (u(x))^{n} dx}} = \displaystyle{\frac{(u(x))^{n+1}}{n+1}} + C, (n \neq -1)\\
\displaystyle{\int{\frac{u'(x)}{u(x)} dx}} = Ln|u(x)| + C\\
\displaystyle{\int{u'(x) e^{u(x)} dx}} = e^{u(x)} + C\\
\displaystyle{\int{u'(x) a^{u(x)} dx}} = \displaystyle{\frac{a^{u(x)}}{Ln|a|}} + C\\
\displaystyle{\int{u'(x) cos(u(x)) dx}} = sen(u(x)) + C\\
\displaystyle{\int{u'(x) sen(u(x)) dx}} = -cos(u(x)) + C\\
\displaystyle{\int{u'(x)\left(1+tg^2(u(x))\right) dx}} = \displaystyle{\int{\frac{u'(x)}{cos^2(u(x))} dx}} = tg(u(x)) + C\\
\displaystyle{\int{u'(x)\left(1+cotg^2(u(x))\right) dx}} = \displaystyle{\int{\frac{u'(x)}{sen^2(u(x))} dx}} = -cotg(u(x)) + C\\
\displaystyle{\int{\frac{u'(x)}{\sqrt[]{1-u^2(x)}} dx}} = arcsen(u(x)) + C\\
\displaystyle{\int{\frac{u'(x)}{1+u^2(x)} dx}} = arctg(u(x)) + C\\
\end{array}\right.
$$
Linealidad de la integral
$$
\left.\begin{array}{ll}
\displaystyle{\int{\left(\alpha f(x) \pm \beta g(x)\right)dx}}=\displaystyle{\alpha\int{f(x)dx}} \pm \displaystyle{\beta\int{g(x)dx}} & \alpha, \beta \in \mathbb{R}\\
\end{array}\right.
$$
Método de integración integración por partes
Sean \(f(x)\), \(g(x)\) continuas en \([a,b]\). Sea \(G(x)\) una primitiva de \(g(x)\):
$$
\displaystyle{\int{f(x)g(x)dx}}=f(x)G(x)-\displaystyle{\int{f'(x)G(x)dx}}
$$
Integral definida
Sea \(f(x)\) una función continua en un intervalo \([a,b]\) y \(F(x)\) una primitiva de \(f(x)\). La integral definidia de \(f(x)\) en el intervalo \([a,b]\) se denota por \(\displaystyle{\int_{a}^{b}{f(x)dx}}.\)
Propiedades:
-
Regla de Barrow:
\(\displaystyle{\int_{a}^{b}{f(x)dx}}={\left[F(x)\right]}_{x=a}^{x=b}=F(b)-F(a)\)
\(\displaystyle{\int_{a}^{b}{f(x)dx}} \in \mathbb{R}\), no depende de la primitiva \(F(x)\) (la constante C se elimina al restar). \(\displaystyle{\int_{a}^{b}{f(x)dx}}=-\displaystyle{\int_{b}^{a}{f(x)dx}}\) -
Aditividad en el intervalo:
Sea \(f(x)\) continua en \([a,b]\), \(c \in [a,b] \Rightarrow \displaystyle{\int_{a}^{b}{f(x)dx}}=\displaystyle{\int_{a}^{c}{f(x)dx}}+\displaystyle{\int_{c}^{b}{f(x)dx}}\)
-
Monotonía en el intervalo:
Sean \(f(x)\), \(g(x)\) continuas en \([a,b]\), \(f(x) \leq g(x), x \in [a,b] \Rightarrow \displaystyle{\int_{a}^{b}{f(x)dx}} \leq \displaystyle{\int_{a}^{b}{g(x)dx}}\)
Interpretación geométrica de la integral definida de una función en un intervalo cerrado
La integral definida coincide con el área sólo cuando la función es positiva, es decir, está por encima del \(\hbox{eje X}\). Cuando la función en negativa, la integral también es negativa, dándonos el área cambiada de signo. Y cuando la función cambia de signo, es decir, está por encima y por debajo del \(\hbox{eje X}\), la integral es igual a la resta entre las áreas de las regiones superiores y las áreas de las regiones inferiores.
Área encerrada entre una curva y el eje X
Resolvemos la ecuación \(f(x)=0\). Supongamos que los ceros obtenidos en el intervalo \([a,b]\), ordenados de menor a mayor, son \(x=x_1,x_2,\cdots,x_n.\) Calculamos las integrales: \(\displaystyle{\int_{a}^{x_1}{f(x)dx}},\displaystyle{\int_{x_1}^{x_2}{f(x)dx}}, \cdots, \displaystyle{\int_{x_n}^{b}{f(x)dx}}.\) El área es la suma de los valores absolutos de cada una de las integrales anteriores.
Área encerrada entre dos curvas
Dadas las funciones \(f(x)\) y \(g(x)\), \(f(x) \geq g(x)\), para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):
Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a\) y \(x=b\). Calculamos la integral: \(\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}\).
Aplicando la linealidad de la integral y teniendo en cuenta que \(\displaystyle{\int_{a}^{b}{f(x)dx}}=Área(\mathbf{R_1})\) y \(\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_2})\):
$$Área(\mathbf{R})=\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}=\displaystyle{\int_{a}^{b}{f(x)dx}}-\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_1})-Área(\mathbf{R_2})$$
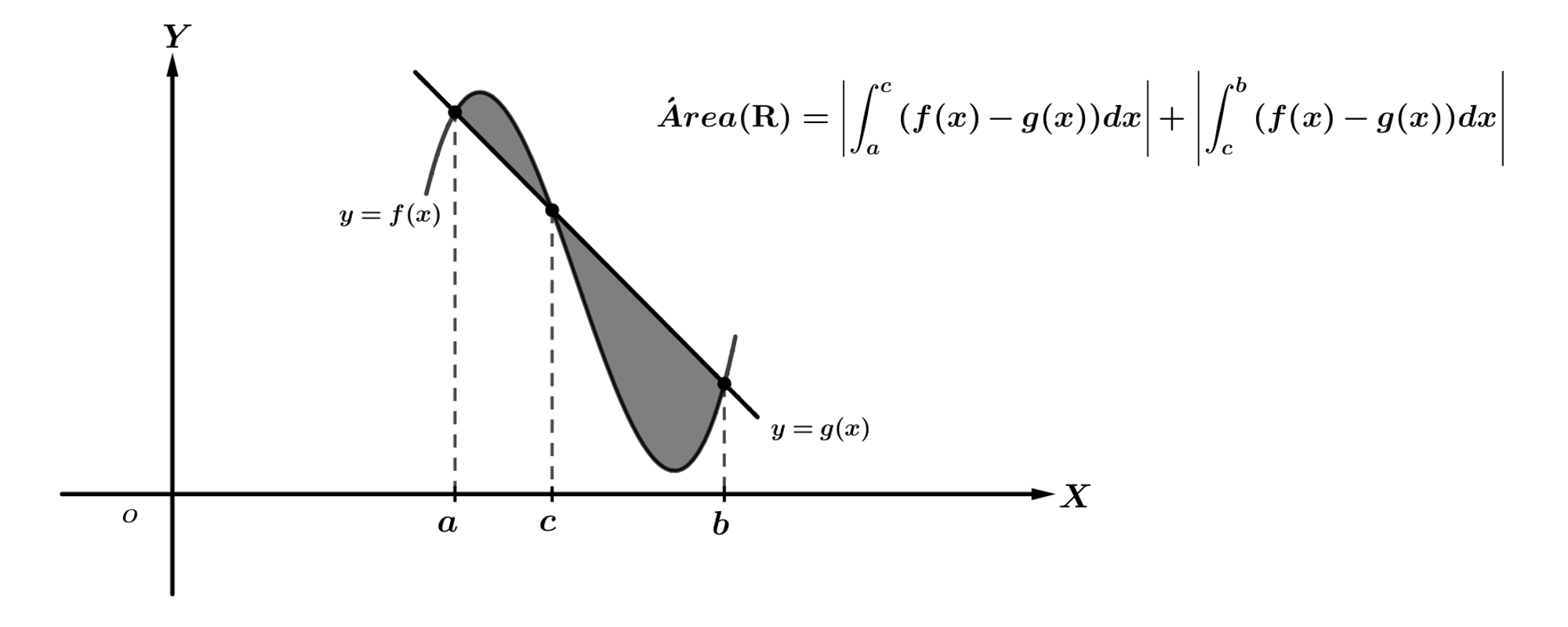
En general, para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):
Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a,x=c\) y \(x=b\). Calculamos las integrales: \(\displaystyle{\int_{a}^{c}{\left(f(x)-g(x)\right)dx}}\) y \(\displaystyle{\int_{c}^{b}{\left(f(x)-g(x)\right)dx}}\). El área es la suma de los valores absolutos de las integrales anteriores (de ese modo no hay que tener en cuenta qué función es mayor y menor en cada intervalo).
|
|