
|
|
|
|
Cuestiones teóricas: Integral indefinida. Integral definida. Aplicaciones de la integral
|
Cuestión (#1)
Prueba que si \(F: \mathbb{D} \rightarrow \mathbb{R}\) es una primitiva de la función \(f\), entonces lo es también la función \(x \in \mathbb{D} \rightarrow F(x)+C\), donde \(C\) es una constante cualquiera.
Si \(F(x)\) es una primitiva de \(f(x) \Rightarrow F'(x)=f(x)\)
Aplicando la linealidad de la derivada:
\(\left(F(x)+C\right)'=F'(x)+C'=f(x)+0=f(x) \Rightarrow F(x)+C\) es también una primitiva de \(f(x)\)
|
Cuestión (#2)
Consideremos la función \(f\) definida por \(f(x)=\displaystyle{\frac{1}{x}}, x \neq 0\). ¿Es una primitiva de \(f\) la función \(F\) definida por \(F(x)=Ln(x), x >0\)?
No, ya que \(F'(x)=\left(Ln(x)\right)'=\displaystyle{\frac{1}{x}}, x >0\) es la rama derecha de la hipérbola \(y=\displaystyle{\frac{1}{x}}\), y sin embargo, la función dada \(y=\displaystyle{\frac{1}{x}}, x \neq 0\), es la hipérbola completa.
|
Cuestión (#3)
Dos funciones \(f\) y \(g\) tienen la misma función derivada.
¿Es entonces \(f-g\) una función constante? ¿Es \(f-g\) constante en cada intervalo del dominio de derivabilidad?
Si dos funciones \(f\) y \(g\) tienen la misma función derivada, entonces se diferencian en una constante:
\(f'(x)=g'(x) \Rightarrow \displaystyle{\int{f'(x)dx}}=\displaystyle{\int{g'(x)dx}} \Rightarrow f(x)+C_1=g(x)+C_2 \Rightarrow f(x)-g(x)=C_2-C_1 \Rightarrow f(x)-g(x)=C\)
No, ya que puede ser una función a trozos y ambas funciones se diferenciarían en una constante en cada trozo, por lo que en cada trozo sería constante, pero ambas constantes puden ser distintas. Sí, en cada intervalo del dominio de derivabilidad sería constante.
|
Cuestión (#4)
Una función coincide en todo punto con su derivada. ¿De qué función puede tratarse?
|
Cuestión (#5)
Comprueba que si \(n \neq 1\), \(\displaystyle{\int{\frac{1}{x^n}dx}}=\displaystyle{\frac{-1}{(n-1)x^{n-1}}}+C\)
Sea \(F(x)=\displaystyle{\frac{-1}{(n-1)x^{n-1}}}+C, n \neq 1\).
Sea \(F'(x)=\left(\displaystyle{\frac{-1}{(n-1)x^{n-1}}}+C\right)'=\left(\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{1}{x^{n-1}}}\right)'+C'=\displaystyle{\frac{-1}{(n-1)}} \cdot \left(\displaystyle{\frac{1}{x^{n-1}}}\right)'+0=\).
\(=\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{1' \cdot x^{n-1} - 1 \cdot (n-1)x^{n-1-1}}{\left(x^{n-1}\right)^2}}=\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{0 \cdot x^{n-1} - 1 \cdot (n-1)x^{n-2}}{x^{2(n-1)}}}=\).
\(=\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{-(n-1)x^{n-2}}{x^{2n-2}}}=\displaystyle{\frac{(n-1)x^{n-2}}{(n-1)x^{2n-2}}}=\displaystyle{\frac{1}{x^{(2n-2)-(n-2)}}}=\displaystyle{\frac{1}{x^{2n-2-n+2}}}=\displaystyle{\frac{1}{x^{n}}}, n \neq 1\).
|
Cuestión (#6)
Una primitiva de la función continua \(f(x)\) es la función \(F(x)\). Obtén una primitiva de \(f\) que pase por el origen de coordenadas.
Si una primitiva de la función continua \(f(x)\) es la función \(F(x) \Rightarrow\) La función \(y=F(x)+C\), \(C\) constante, también es una primitiva de \(f(x)\).
Si pasa por el punto \((0,0)\), sustituyendo en \(y=F(x)+C\) se obtiene que: \(F(0)+C=0 \Rightarrow C=-F(0)\)
Por tanto, la primitiva buscada es \(y=F(x)-F(0)\).
|
Cuestión (#7)
Si la gráfica de una función \(y=f(x)\) es una línea recta. ¿Cómo es la gráfica de una primitiva de ella?
La ecuación de una recta es \(f(x)=ax+b, a \neq 0\).
Una primitiva suya es de la forma \(F(x)=\displaystyle{\int{\left(ax+b\right)dx}}, a \neq 0\).
\(F(x)=\displaystyle{\int{\left(ax+b\right)dx}}=\displaystyle{a\int{xdx}}+\displaystyle{b\int{1dx}}=\displaystyle{a\left(\frac{x^2}{2}\right)}+bx+C=\displaystyle{\frac{ax^2}{2}}+bx+C, a \neq 0\)
Por tanto, la gráfica de una primitiva suya es una parábola.
|
Cuestión (#8)
Obtén una primitiva de la función representada a continuación:
La ecuación de la recta que pasa por los puntos \(A(-2,0)\) y \(B(0,2)\) es \(y=x+2\).
\(\overrightarrow{AB}=B-A=(0,2)-(-2,0)=(2,2) \Rightarrow \left\{\begin{array}{l}
m=\displaystyle{\frac{2}{2}}=1\\
n=2\\
\end{array}\right.\)
Una primitiva suya es de la forma \(F(x)=\displaystyle{\int{\left(x+2\right)dx}}\).
\(F(x)=\displaystyle{\int{\left(x+2\right)dx}}=\displaystyle{\int{xdx}}+\displaystyle{2\int{1dx}}=\displaystyle{\frac{x^2}{2}}+2x+C\)
Por tanto, la gráfica de una primitiva suya es una parábola \(y=\displaystyle{\frac{x^2}{2}}+2x\) y las traslaciones verticales de \(C\) unidades de la misma.
|
Cuestión (#9)
Comprueba que \(\displaystyle{\int{2x cos(x)dx}} \neq x^2sen(x)+C\)
Sea \(F(x)=x^2sen(x)+C\) y \(f(x)=2x cos(x)\)
Queremos comprobar que \(F(x) \neq \displaystyle{\int{f(x)dx}} \Rightarrow F'(x) \neq f(x)\)
Aplicando la regla de la cadena:
\(F'(x)=\left(x^2sen(x)+C\right)'= \left(x^2sen(x)\right)'+C'= 2x sen(x)+x^2 (-cos(x))+0=\)
\(= 2x sen(x)-x^2 cos(x) \neq 2x cos(x) = f(x)\)
|
Cuestión (#10)
Tras analizar la cuestión anterior, ¿Es la integral indefinida de un producto el producto de las integrales indefinidas de los factores?
No, ya que la Cuestión (#9) es un ejemplo donde no se cumple. De ser cierto, debería cumplirse siempre.
|
Cuestión (#11)
Halla \(f(x)\) sabiendo que:
- \(\displaystyle{\int{f(x)dx}}=x^3-x+C\)
- \(\displaystyle{\int{f(x)dx}}=Ln(3x+1)+C\)
- \(\displaystyle{\int{f(x)dx}}=sen(2x+1)+C\)
- \(F(x)=x^3-x+C \Rightarrow f(x)=F'(x)=\left(x^3-x+C\right)'=3x^2-1+0=3x^2-1\)
- \(F(x)=Ln(3x+1)+C \Rightarrow f(x)=F'(x)=\left(Ln(3x+1)+C\right)'=\displaystyle{\frac{3}{3x+1}}+0=\displaystyle{\frac{3}{3x+1}}\)
- \(F(x)=sen(2x+1)+C \Rightarrow f(x)=F'(x)=\left(sen(2x+1)+C\right)'=2cos(2x+1)+0=2cos(2x+1)\)
|
Cuestión (#12)
Obtén la función \(u\) sabiendo que \(\displaystyle{\int{2xcos(x^2)dx}}=u(x^2)+C\)
\(u(x)=sen(x)\)
Aplicando la regla de la cadena: \(\left(sen(x^2)+C\right)'=2xcos(x^2)\).
|
Cuestión (#13)
Dada la función \(f: \mathbb{R}-\{0\} \rightarrow \mathbb{R}\) definida por
\(f(x)= \left\{\begin{array}{lcc}
1 & si & x < 0\\
2x & si & x > 0\\
\end{array}\right.\), encuentra una función continua \(F: \mathbb{R} \rightarrow \mathbb{R}\) tal que
\(F(x)\) se obtiene integrando cada uno de los trozos de la función \(f(x)\):
\(F(x)=\left\{\begin{array}{lcc}
x+C_1 & si & x < 0\\
x^2+C_2 & si & x > 0\\
\end{array}\right.\)
Como \(F(x)\) es continua en \(x=0\):
- \(F(0)=5\)
- \(\left\{\begin{array}{l}
F(0^{-}=\displaystyle{\lim_{x \rightarrow 0^{-}} (x+C_1)}=0+C_1=C_1\\
F(0^{+}=\displaystyle{\lim_{x \rightarrow 0^{+}} (x^2+C_2)}=0^2+C_2=C_2\\
\end{array}\right.\Rightarrow C_1=C_2=5\)
\(F(x)=\left\{\begin{array}{lcc}
x+5 & si & x \leq 0\\
x^2+5 & si & x > 0\\
\end{array}\right.\)
Pero \(F(x)\) no es derivable para \(x=0\), ya que su derivada es \(f(x)\) y no es continua para \(x=0\) al no estar definida para ese valor.
|
Cuestión (#14)
Demuestra que \(f: \mathbb{R} \rightarrow \mathbb{R}\) definida por
\(f(x)= \left\{\begin{array}{lcc}
1 & si & x \leq 0\\
2x & si & x > 0\\
\end{array}\right.\), no es la función derivada de ninguna \(F: \mathbb{R} \rightarrow \mathbb{R}\).
Si cierta función \(F(x)\) fuera una primitiva de \(f(x)\), entonces \(F(x)\) sería derivable y \(F'(x)=f(x)\).
Como ser derivable implica ser continua, entonces \(f(x)\) sería continua en \(\mathbb{R}\), pero \(f(x)\) no es continua en \(x=0\) porque no coinciden los límites laterales cuando \(x \rightarrow 0\).
Continuidad en \(x=0\)
\(\left. \begin{array}{l}
1) f(0)=1\\
2) \displaystyle\lim_{x \rightarrow 0} f(x)=
\left \{ \begin{array}{l}
\displaystyle\lim_{x \rightarrow 0^{-}} 1=1\\
\displaystyle\lim_{x \rightarrow 0^{+}} 2x=2 \cdot 0=0\\
\end{array}
\right.\\
\end{array}
\right\} \Rightarrow f(x)\) no es continua en \(x=0\)
|
Algunos resultados teóricos
Integrales:
Integral indefinida. Integrales inmediatas
Dada una función \(f(x)\) continua, se define una primitiva (o integral) de \(f(x)\), como una función \(F(x)\) tal que \(F'(x)=f(x)\).
En ese caso, decimos que \(F(x)=\displaystyle{\int{f(x) dx}} + C\), donde \( C \in \mathbb{R} \) (Notación de Leibnitz)
$$
\left\{\begin{array}{l}
\displaystyle{\int{k dx}} = kx + C\\
\displaystyle{\int{x^{n} dx}} = \displaystyle{\frac{x^{n+1}}{n+1}} + C, (n \neq -1)\\
\displaystyle{\int{\frac{1}{x} dx}} = Ln|x| + C\\
\displaystyle{\int{e^{x} dx}} = e^{x} + C\\
\displaystyle{\int{a^{x} dx}} = \displaystyle{\frac{a^{x}}{Ln|a|}} + C\\
\displaystyle{\int{cos(x) dx}} = sen(x) + C\\
\displaystyle{\int{sen(x) dx}} = -cos(x) + C\\
\displaystyle{\int{\left(1+tg^2(x)\right) dx}} = \displaystyle{\int{\frac{1}{cos^2(x)} dx}} = tg(x) + C\\
\displaystyle{\int{\left(1+cotg^2(x)\right) dx}} = \displaystyle{\int{\frac{1}{sen^2(x)} dx}} = -cotg(x) + C\\
\displaystyle{\int{\frac{1}{\sqrt[]{1-x^2}} dx}} = arcsen(x) + C\\
\displaystyle{\int{\frac{1}{1+x^2} dx}} = arctg(x) + C\\
\end{array}\right.
$$
Métodos de Integración: Integral de formas compuestas (Cambio de variable)
$$
\left\{\begin{array}{l}
\displaystyle{\int{u'(x) (u(x))^{n} dx}} = \displaystyle{\frac{(u(x))^{n+1}}{n+1}} + C, (n \neq -1)\\
\displaystyle{\int{\frac{u'(x)}{u(x)} dx}} = Ln|u(x)| + C\\
\displaystyle{\int{u'(x) e^{u(x)} dx}} = e^{u(x)} + C\\
\displaystyle{\int{u'(x) a^{u(x)} dx}} = \displaystyle{\frac{a^{u(x)}}{Ln|a|}} + C\\
\displaystyle{\int{u'(x) cos(u(x)) dx}} = sen(u(x)) + C\\
\displaystyle{\int{u'(x) sen(u(x)) dx}} = -cos(u(x)) + C\\
\displaystyle{\int{u'(x)\left(1+tg^2(u(x))\right) dx}} = \displaystyle{\int{\frac{u'(x)}{cos^2(u(x))} dx}} = tg(u(x)) + C\\
\displaystyle{\int{u'(x)\left(1+cotg^2(u(x))\right) dx}} = \displaystyle{\int{\frac{u'(x)}{sen^2(u(x))} dx}} = -cotg(u(x)) + C\\
\displaystyle{\int{\frac{u'(x)}{\sqrt[]{1-u^2(x)}} dx}} = arcsen(u(x)) + C\\
\displaystyle{\int{\frac{u'(x)}{1+u^2(x)} dx}} = arctg(u(x)) + C\\
\end{array}\right.
$$
Linealidad de la integral
$$
\left.\begin{array}{ll}
\displaystyle{\int{\left(\alpha f(x) \pm \beta g(x)\right)dx}}=\displaystyle{\alpha\int{f(x)dx}} \pm \displaystyle{\beta\int{g(x)dx}} & \alpha, \beta \in \mathbb{R}\\
\end{array}\right.
$$
Método de integración integración por partes
Sean \(f(x)\), \(g(x)\) continuas en \([a,b]\). Sea \(G(x)\) una primitiva de \(g(x)\):
$$
\displaystyle{\int{f(x)g(x)dx}}=f(x)G(x)-\displaystyle{\int{f'(x)G(x)dx}}
$$
Integral definida
Sea \(f(x)\) una función continua en un intervalo \([a,b]\) y \(F(x)\) una primitiva de \(f(x)\). La integral definidia de \(f(x)\) en el intervalo \([a,b]\) se denota por \(\displaystyle{\int_{a}^{b}{f(x)dx}}.\)
Propiedades:
-
Regla de Barrow:
\(\displaystyle{\int_{a}^{b}{f(x)dx}}={\left[F(x)\right]}_{x=a}^{x=b}=F(b)-F(a)\)
\(\displaystyle{\int_{a}^{b}{f(x)dx}} \in \mathbb{R}\), no depende de la primitiva \(F(x)\) (la constante C se elimina al restar). \(\displaystyle{\int_{a}^{b}{f(x)dx}}=-\displaystyle{\int_{b}^{a}{f(x)dx}}\) -
Aditividad en el intervalo:
Sea \(f(x)\) continua en \([a,b]\), \(c \in [a,b] \Rightarrow \displaystyle{\int_{a}^{b}{f(x)dx}}=\displaystyle{\int_{a}^{c}{f(x)dx}}+\displaystyle{\int_{c}^{b}{f(x)dx}}\)
-
Monotonía en el intervalo:
Sean \(f(x)\), \(g(x)\) continuas en \([a,b]\), \(f(x) \leq g(x), x \in [a,b] \Rightarrow \displaystyle{\int_{a}^{b}{f(x)dx}} \leq \displaystyle{\int_{a}^{b}{g(x)dx}}\)
Interpretación geométrica de la integral definida de una función en un intervalo cerrado
La integral definida coincide con el área sólo cuando la función es positiva, es decir, está por encima del \(\hbox{eje X}\). Cuando la función en negativa, la integral también es negativa, dándonos el área cambiada de signo. Y cuando la función cambia de signo, es decir, está por encima y por debajo del \(\hbox{eje X}\), la integral es igual a la resta entre las áreas de las regiones superiores y las áreas de las regiones inferiores.
Área encerrada entre una curva y el eje X
Resolvemos la ecuación \(f(x)=0\). Supongamos que los ceros obtenidos en el intervalo \([a,b]\), ordenados de menor a mayor, son \(x=x_1,x_2,\cdots,x_n.\) Calculamos las integrales: \(\displaystyle{\int_{a}^{x_1}{f(x)dx}},\displaystyle{\int_{x_1}^{x_2}{f(x)dx}}, \cdots, \displaystyle{\int_{x_n}^{b}{f(x)dx}}.\) El área es la suma de los valores absolutos de cada una de las integrales anteriores.
Área encerrada entre dos curvas
Dadas las funciones \(f(x)\) y \(g(x)\), \(f(x) \geq g(x)\), para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):
Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a\) y \(x=b\). Calculamos la integral: \(\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}\).
Aplicando la linealidad de la integral y teniendo en cuenta que \(\displaystyle{\int_{a}^{b}{f(x)dx}}=Área(\mathbf{R_1})\) y \(\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_2})\):
$$Área(\mathbf{R})=\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}=\displaystyle{\int_{a}^{b}{f(x)dx}}-\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_1})-Área(\mathbf{R_2})$$
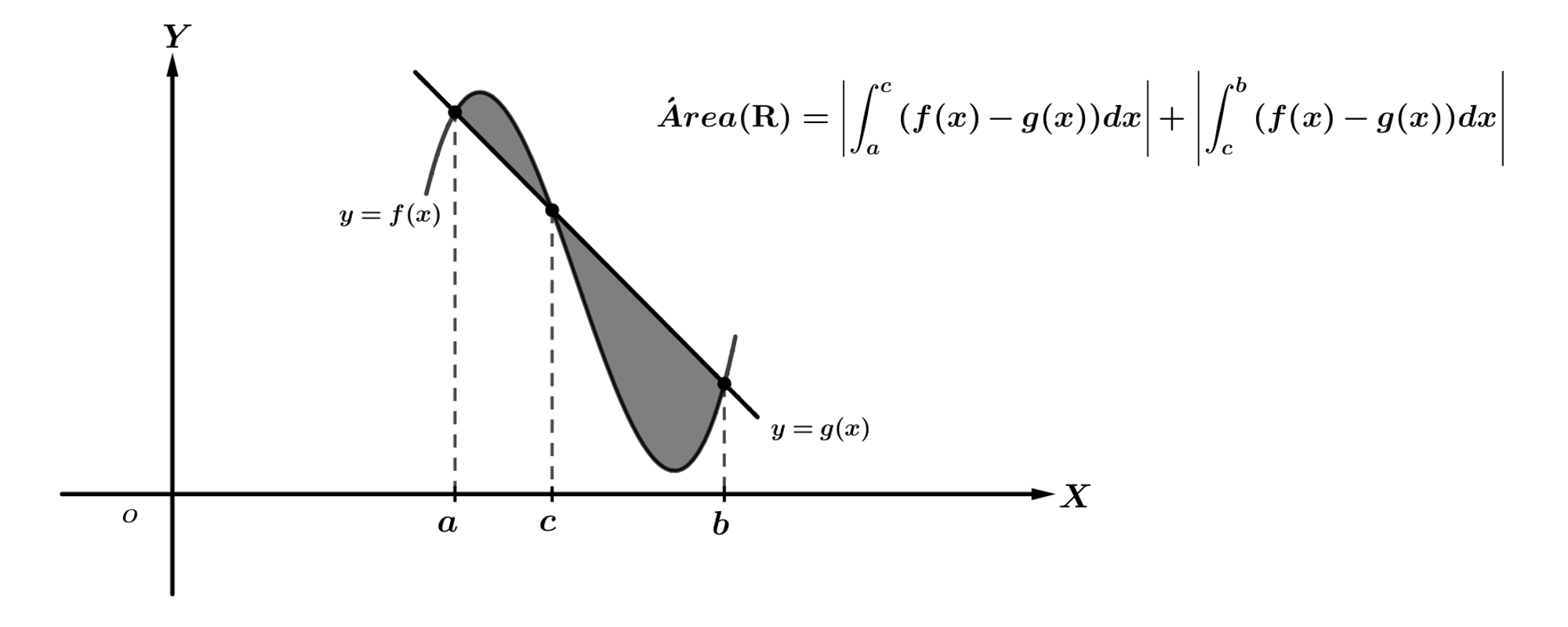
En general, para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):
Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a,x=c\) y \(x=b\). Calculamos las integrales: \(\displaystyle{\int_{a}^{c}{\left(f(x)-g(x)\right)dx}}\) y \(\displaystyle{\int_{c}^{b}{\left(f(x)-g(x)\right)dx}}\). El área es la suma de los valores absolutos de las integrales anteriores (de ese modo no hay que tener en cuenta qué función es mayor y menor en cada intervalo).
|
|