Obtén una función cuya derivada sea:

1. \(f(x)=1\)
2. \(f(x)=3x^2+1\)
3. \(f(x)=cos(x)-1\)
4. \(f(x)=3e^{x}-x^2\)
5. \(f(x)=\displaystyle{\frac{2}{x}}\), si \(x>0\)

1. \(F(x)=\displaystyle{\int{1dx}}=x+C\)

2. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{(3x^2+1)dx}}=3\displaystyle{\int{x^2dx}}+\displaystyle{\int{1dx}}=\displaystyle{3 \cdot \frac{x^3}{3}}+x+C=x^3+x+C\)

3. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{(cos(x)-1)dx}}=\displaystyle{\int{cos(x)dx}}-\displaystyle{\int{1dx}}=sen(x)-x+C\)

4. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{(3e^{x}-x^2)dx}}=3\displaystyle{\int{e^{x}dx}}-\displaystyle{\int{x^2dx}}=3e^{x}-\displaystyle{\frac{x^3}{3}}+C\)

5. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{\frac{2}{x}}dx}=2\displaystyle{\int{\frac{1}{x}}dx}=2Ln(x)+C\), si \(x > 0\)

Halla una primitiva de la función \(y=2x-1\) que corta al eje de abscisas para \(x=-1\).

Aplicando la linealidad de la integral:

\(F(x)=\displaystyle{\int{(2x-1)dx}}=\displaystyle{2\int{xdx}}-\displaystyle{\int{1dx}}=\displaystyle{2 \cdot \frac{x^2}{2}}-x+C=x^2-x+C\)

Si corta al eje de abscisas \(\hbox{(Eje X)}\) en \(x=-1\), entonces, pasa por el punto \((-1,0)\). Por tanto, sustituyendo en \(F(x)\) se obtiene que:

\(F(-1)=(-1)^2-(-1)+C=0 \Rightarrow 2+C=0 \Rightarrow C=-2\)

Obtén una primitiva de las siguientes funciones:

1. \(f(x)=x-1\) que pasa por \(P(2,1)\).
2. \(f(x)=x-e^{x}\) que pasa por el origen de coordenadas.
3. \(f(x)=3x^2+2x+1\) que se anula para \(x=1\).

1. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{(x-1)dx}}=\displaystyle{\int{xdx}}-\displaystyle{\int{1dx}}=\displaystyle{\frac{x^2}{2}}-x+C\)

   Si pasa por el punto \((2,1)\), sustituyendo en \(F(x)\) se obtiene que:

   \(F(2)=\displaystyle{\frac{2^2}{2}}-2+C=1 \Rightarrow 2-2+C=1 \Rightarrow C=1\)

2. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{(x-e^{x})dx}}=\displaystyle{\int{xdx}}-\displaystyle{\int{e^{x}dx}}=\displaystyle{\frac{x^2}{2}}-e^{x}+C\)

   Si pasa por el punto \((0,0)\), sustituyendo en \(F(x)\) se obtiene que:

   \(F(0)=\displaystyle{\frac{0^2}{2}}-e^{0}+C=0 \Rightarrow 0-1+C=0 \Rightarrow C=1\)

3. Aplicando la linealidad de la integral:

   \(F(x)=\displaystyle{\int{(3x^2+2x+1)dx}}=\displaystyle{3\int{x^2dx}}+\displaystyle{2\int{xdx}}+\displaystyle{\int{1dx}}=\displaystyle{3 \cdot \frac{x^3}{3}}+\displaystyle{2 \cdot \frac{x^2}{2}}+x+C=x^3+x^2+x+C\)

   Si se anula para \(x=1 \Rightarrow\) Pasa por el punto \((1,0)\). Por tanto, sustituyendo en \(F(x)\) se obtiene que:

   \(F(1)=1^3+1^2+1+C=0 \Rightarrow 3+C=0 \Rightarrow C=-3\)

Obtén la primitiva de la función \(y=x^2-sen(x)\) que pasa por el origen de coordenadas.

Aplicando la linealidad de la integral:

\(F(x)=\displaystyle{\int{(x^2-sen(x))dx}}=\displaystyle{\int{x^2dx}}-\displaystyle{\int{sen(x)dx}}=\displaystyle{\frac{x^3}{3}}-(-cos(x))+C=\displaystyle{\frac{x^3}{3}}+cos(x)+C\)

Si pasa por el punto \((0,0)\), sustituyendo en \(F(x)\) se obtiene que:

\(F(0)=\displaystyle{\frac{0^3}{3}}+cos(0)+C=0 \Rightarrow 0+1+C=0 \Rightarrow C=-1\)

Obtén la expresión de una función \(f\) tal que \(f'(x)=x^2+2e^{x}\) sabiendo que se anula para \(x=0\).

Aplicando la linealidad de la integral:

\(f(x)=\displaystyle{\int{f'(x)dx}}=\displaystyle{\int{(x^2+2e^{x})dx}}=\displaystyle{\int{x^2dx}}+2\displaystyle{\int{e^{x}dx}}=\displaystyle{\frac{x^3}{3}}+2e^{x}+C=\)

Si se anula para \(x=0 \Rightarrow \) Pasa por el punto \((0,0)\). Por tanto, sustituyendo en \(F(x)\) se obtiene que:

\(F(0)=\displaystyle{\frac{0^3}{3}}+2e^{0}+C=0 \Rightarrow 0+2 \cdot 1+C=0 \Rightarrow 2+C=0 \Rightarrow C=-2\)

Obtén \(f(x)\) sabiendo que tiene un extremo relativo en el punto \((-1,1)\) y que su derivada segunda viene dada por \(f''(x)=6x-12\).

Aplicando la linealidad de la integral:

\(f'(x)=\displaystyle{\int{f''(x)dx}}=\displaystyle{\int{(6x-12)dx}}=\displaystyle{6\int{xdx}}-12\displaystyle{\int{1dx}}=\displaystyle{\frac{6x^2}{2}}-12x+C_1=\)

\(=3x^2-12x+C_1\)

\(f(x)=\displaystyle{\int{f'(x)dx}}=\displaystyle{\int{(3x^2-12x+C_1)dx}}=\displaystyle{3\int{x^2dx}}-\displaystyle{12\int{xdx}}+\displaystyle{C_1\int{1dx}}=\)

\(=\displaystyle{\frac{3x^3}{3}}-\displaystyle{\frac{12x^2}{2}}+\displaystyle{C_1x}+C_2=x^3-6x^2+C_1x+C_2\)

Si tiene un extremo relativo en el punto \((-1,1) \Rightarrow \left\{\begin{array}{l} f(-1)=1\\ f'(-1)=0\\ \end{array}\right.\)

Por tanto, sustituyendo en \(f(x)\) se obtiene que:

\(f(-1)=1 \Rightarrow (-1)^3-6 \cdot (-1)^2+C_1 \cdot (-1)+C_2=1 \Rightarrow -1-6-C_1+C_2=1 \Rightarrow C_2-C_1=8\) \((*)\)

Y sustituyendo en \(f'(x)\) se obtiene que:

\(f'(-1)=0 \Rightarrow 3(-1)^2-12 \cdot (-1)+C_1=0 \Rightarrow 3+12+C_1=0 \Rightarrow C_1=-15\)

Y sustituyendo en \((*)\) se obtiene que: \(C_2-(-15)=8 \Rightarrow C_2+15=8 \Rightarrow C_2=-7\)

Por tanto, \(f(x)=x^3-6x^2-15x-7\)

Determina la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) que para \(x=1\) tiene de tangente a \(x+12y=13\) y tal que \(f''(x)=x^2-1\).

Aplicando la linealidad de la integral:

\(f'(x)=\displaystyle{\int{f''(x)dx}}=\displaystyle{\int{(x^2-1)dx}}=\displaystyle{\int{x^2dx}}-\displaystyle{\int{1dx}}=\displaystyle{\frac{x^3}{3}}-x+C_1\)

\(f(x)=\displaystyle{\int{f'(x)dx}}=\displaystyle{\int{\left(\displaystyle{\frac{x^3}{3}}-x+C_1\right)dx}}=\displaystyle{\frac{x^3}{3}}-\displaystyle{\int{xdx}}+\displaystyle{C_1\int{1dx}}=\)

\(=\displaystyle{\frac{x^4}{12}}-\displaystyle{\frac{x^2}{2}}+\displaystyle{C_1x}+C_2\)

Si para \(x=1\) la recta tangente es \(x+12y=13 \Rightarrow y=-\displaystyle{\frac{1}{12}}x+\displaystyle{\frac{13}{12}} \Rightarrow m=-\displaystyle{\frac{1}{12}}\)

La coordenada \(y\) del punto de tangencia la obtenemos sustituyendo en la ecuación de la recta tangente:

Si \(x=1 \Rightarrow y=-\displaystyle{\frac{1}{12}}+\displaystyle{\frac{13}{12}}=1 \Rightarrow P(1,1)\)

Por el punto de tangencia ambas gráficas pasan, por tanto: \(\left\{\begin{array}{l} f(1)=1\\ f'(1)=-\displaystyle{\frac{1}{12}}\\ \end{array}\right.\)

Por tanto, sustituyendo en \(f(x)\) se obtiene que:

\(f(1)=1 \Rightarrow \displaystyle{\frac{1^4}{12}}-\displaystyle{\frac{1^2}{2}}+\displaystyle{C_1 \cdot 1}+C_2=\displaystyle{\frac{1}{12}}-\displaystyle{\frac{1}{2}}+C_1+C_2=1 \Rightarrow C_1+C_2=1-\displaystyle{\frac{1}{12}}+\displaystyle{\frac{1}{2}} \Rightarrow C_1+C_2=\displaystyle{\frac{17}{12}}\) \((*)\)

Y sustituyendo en \(f'(x)\) se obtiene que:

\(f'(1)=-\displaystyle{\frac{1}{12}} \Rightarrow \displaystyle{\frac{1^3}{3}}-1+C_1=-\displaystyle{\frac{1}{12}} \Rightarrow C_1=-\displaystyle{\frac{1}{12}}-\displaystyle{\frac{1}{3}}+1 \Rightarrow C_1=\displaystyle{\frac{7}{12}}\)

Y sustituyendo en \((*)\) se obtiene que: \(\displaystyle{\frac{7}{12}}+C_2=\displaystyle{\frac{17}{12}} \Rightarrow C_2=\displaystyle{\frac{17}{12}}-\displaystyle{\frac{7}{12}} \Rightarrow C_2=\displaystyle{\frac{10}{12}}=\displaystyle{\frac{5}{6}}\)

Por tanto, \(f(x)=\displaystyle{\frac{x^4}{12}}-\displaystyle{\frac{x^2}{2}}+\displaystyle{\frac{7x}{12}}+\displaystyle{\frac{5}{6}}\)

Obtén la primitiva de la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) con \(f(x)= \left\{\begin{array}{lcc} 2x & si & x < 1\\ 2 & si & x \geq 1\\ \end{array}\right.\) que pasa por el punto \(P(1,4)\).

\(F(x)=\displaystyle{\int{f(x)dx}}=\left\{\begin{array}{lcc} \displaystyle{\int{2xdx}} & si & x < 1\\ \displaystyle{\int{2dx}} & si & x \geq 1\\ \end{array}\right.= \left\{\begin{array}{lcc} x^2+C_1 & si & x < 1\\ 2x+C_2 & si & x \geq 1\\ \end{array}\right.\)

Como \(F(x)\) es derivable en \(x=1 \Rightarrow F(x)\) es continua en \(x=1\). Por tanto:

\(\left.\begin{array}{l} 1) f(1)=2+C_2\\ 2) \displaystyle\lim_{x \rightarrow +1} f(x)= \left\{\begin{array}{l} \displaystyle\lim_{x \rightarrow +1^{-}} x^2+C_1=1+C_1\\ \displaystyle\lim_{x \rightarrow +1^{+}} 2x+C_2=2+C_2\\ \end{array}\right.\\ \end{array}\right\} \Rightarrow 1+C_1=2+C_2 \Rightarrow C_1-C_2=1 \)

Como \(F(x)\) pasa por el punto \((1,4)\), sustituyendo en \(F(x)\) se obtiene que:

\(F(1)=4 \Rightarrow 2 \cdot 1+C_2=4 \Rightarrow C_2=2\)

Sustituyendo en la ecuación anterior, se obtiene que: \(C_1-2=1 \Rightarrow C_1=3\)

Por tanto, \(F(x)= \left\{\begin{array}{lcc} x^2+3 & si & x < 1\\ 2x+2 & si & x \geq 1\\ \end{array}\right.\)

Obtén \(\displaystyle{\int{\left|2x-2\right|dx}}\)

¿Qué primitiva pasa por el origen de coordenadas?

\(f(x)=\left|2x-2\right|= \left\{\begin{array}{ccc} 2x-2 & si & 2x-2 \geq 0\\ -(2x-2) & si & 2x-2 < 0\\ \end{array}\right.= \left\{\begin{array}{ccc} 2x-2 & si & x \geq 1\\ -2x+2 & si & x < 1\\ \end{array}\right.\)

\(F(x)=\displaystyle{\int{f(x)dx}}=\left\{\begin{array}{lcc} \displaystyle{\int{\left(2x-2\right)dx}} & si & x \geq 1\\ \displaystyle{\int{\left(-2x+2\right)dx}} & si & x < 1\\ \end{array}\right.= \left\{\begin{array}{lcc} x^2-2x+C_1 & si & x \geq 1\\ -x^2+2x+C_2 & si & x < 1 \\ \end{array}\right.\)

Como \(F(x)\) es derivable en \(x=1 \Rightarrow F(x)\) es continua en \(x=1\). Por tanto:

\(\left.\begin{array}{l} 1) f(1)=C_1-1\\ 2) \displaystyle\lim_{x \rightarrow +1} f(x)= \left\{\begin{array}{l} \displaystyle\lim_{x \rightarrow +1^{-}} -x^2+2x+C_2=C_2+1\\ \displaystyle\lim_{x \rightarrow +1^{+}} x^2-2x+C_1=C_1-1\\ \end{array}\right.\\ \end{array}\right\} \Rightarrow C_2+1=C_1-1 \Rightarrow C_1-C_2=2 \)

Como \(F(x)\) pasa por el punto \((0,0)\), sustituyendo en \(F(x)\) se obtiene que:

\(F(0)=0 \Rightarrow -0^2+2 \cdot 0+C_2=0 \Rightarrow C_2=0\)

Sustituyendo en la ecuación anterior, se obtiene que: \(C_1-0=2 \Rightarrow C_1=2\)

Por tanto, \(F(x)= \left\{\begin{array}{lcc} x^2-2x+2 & si & x \geq 1\\ -x^2+2x & si & x < 1\\ \end{array}\right.\)

Obtén las siguientes integrales indefinidas:

1. \(\displaystyle{\int{5dx}}\)
2. \(\displaystyle{\int{xdx}}\)
3. \(\displaystyle{\int{\frac{1}{x^2}dx}}\)
4. \(\displaystyle{\int{\frac{1}{x}dx}}\)
5. \(\displaystyle{\int{x^3dx}}\)
6. \(\displaystyle{\int{\sqrt[4]{x^5}dx}}\)
7. \(\displaystyle{\int{\sqrt[3]{x^2}dx}}\)
8. \(\displaystyle{\int{\frac{1}{\sqrt[3]{x^5}}}dx}\)

Para resolver cada una de las siguinetes integrales, debemos escribir cada una de las funciones como una potencia de base \(x\):

1. \(\displaystyle{\int{5dx}}=5x+C\)
2. \(\displaystyle{\int{xdx}}=\displaystyle{\frac{x^2}{2}}+C\)
3. \(\displaystyle{\int{\frac{1}{x^2}dx}}=\displaystyle{\int{x^{-2}dx}}=\displaystyle{\frac{x^{-2+1}}{-2+1}}+C=\displaystyle{\frac{x^{-1}}{-1}}+C=\displaystyle{\frac{-1}{x}}+C\)
4. \(\displaystyle{\int{\frac{1}{x}dx}}=Ln\left|x\right|+C\)
5. \(\displaystyle{\int{x^3dx}}=\displaystyle{\frac{x^{3+1}}{3+1}}+C=\displaystyle{\frac{x^{4}}{4}}+C\)
6. \(\displaystyle{\int{\sqrt[4]{x^5}dx}}=\displaystyle{\int{x^{\frac{5}{4}}dx}}=\displaystyle{\frac{x^{\frac{5}{4}+1}}{\frac{5}{4}+1}+C}=\displaystyle{\frac{x^{\frac{9}{4}}}{\frac{9}{4}}+C}=\displaystyle{\frac{4\sqrt[4]{x^9}}{9}}+C=\displaystyle{\frac{4x^2\sqrt[4]{x}}{9}}+C\)
7. \(\displaystyle{\int{\sqrt[3]{x^2}dx}}=\displaystyle{\int{x^{\frac{2}{3}}dx}}=\displaystyle{\frac{x^{\frac{2}{3}+1}}{\frac{2}{3}+1}}+C=\displaystyle{\frac{x^{\frac{5}{3}}}{\frac{5}{3}}+C}=\displaystyle{\frac{3\sqrt[3]{x^5}}{5}}+C=\displaystyle{\frac{3x\sqrt[3]{x^2}}{5}}+C\)
8. \(\displaystyle{\int{\frac{1}{\sqrt[3]{x^5}}}dx}=\displaystyle{\int{\frac{1}{x^{\frac{5}{3}}}}dx}=\displaystyle{\int{x^{-\frac{5}{3}}dx}}=\displaystyle{\frac{x^{-\frac{5}{3}+1}}{-\frac{5}{3}+1}+C}=\displaystyle{\frac{x^{-\frac{2}{3}}}{-\frac{2}{3}}+C}=\displaystyle{\frac{-3}{2x^{\frac{2}{3}}}+C}=\displaystyle{\frac{-3}{2\sqrt[3]{x^2}}}+C\)

Halla las primitivas de los siguientes polinomios:

1. \(f(x)=x^4+4x^3-5x+2\)
2. \(f(x)=3x^3+x^2-7x\)
3. \(f(x)=3x^6+4x^2-1\)
4. \(f(x)=4x^5+3x^4-2x^3+6x^2-9\)
5. \(f(x)=ax^2+bx+c\)

1. Aplicando la linealidad de la integral:

   \(\displaystyle{\int{\left(x^4+4x^3-5x+2\right)dx}}=\displaystyle{\int{x^4dx}}+\displaystyle{4\int{x^3dx}}-\displaystyle{5\int{xdx}}+\displaystyle{2\int{1dx}}=\)

   \(=\displaystyle{\frac{x^5}{5}}+\displaystyle{4 \cdot \frac{x^4}{4}}-\displaystyle{5 \cdot \frac{x^2}{2}}+2x+C=\displaystyle{\frac{x^5}{5}}+x^4-\displaystyle{\frac{5x^2}{2}}+2x+C\)

2. Aplicando la linealidad de la integral:

   \(\displaystyle{\int{\left(3x^3+x^2-7x\right)dx}}=\displaystyle{3\int{x^3dx}}+\displaystyle{\int{x^2dx}}-\displaystyle{7\int{xdx}}=\)

   \(=\displaystyle{3 \cdot \frac{x^4}{4}}+\displaystyle{\frac{x^3}{3}}-\displaystyle{7 \cdot \frac{x^2}{2}}+C=\displaystyle{\frac{3x^4}{4}}+\displaystyle{\frac{x^3}{3}}-\displaystyle{\frac{7x^2}{2}}+C\)

3. Aplicando la linealidad de la integral:

   \(\displaystyle{\int{\left(3x^6+4x^2-1\right)dx}}=\displaystyle{3\int{x^6dx}}+\displaystyle{4\int{x^2dx}}-\displaystyle{\int{1dx}}=\)

   \(=\displaystyle{3 \cdot \frac{x^7}{7}}+\displaystyle{4 \cdot \frac{x^3}{3}}-x+C=\displaystyle{\frac{3x^7}{7}}+\displaystyle{\frac{4x^3}{3}}-x+C\)

4. Aplicando la linealidad de la integral:

   \(\displaystyle{\int{\left(4x^5+3x^4-2x^3+6x^2-9\right)dx}}=\)

   \(=\displaystyle{4\int{x^5dx}}+\displaystyle{3\int{x^4dx}}-\displaystyle{2\int{x^3dx}}+\displaystyle{6\int{x^2dx}}-\displaystyle{9\int{1dx}}=\)

   \(=\displaystyle{4 \cdot \frac{x^6}{6}}+\displaystyle{3 \cdot \frac{x^5}{5}}-\displaystyle{2 \cdot \frac{x^4}{4}}+\displaystyle{6 \cdot \frac{x^3}{3}}-9x+C=\)

   \(=\displaystyle{\frac{4x^6}{6}}+\displaystyle{\frac{3x^5}{5}}-\displaystyle{\frac{2x^4}{4}}+\displaystyle{\frac{6x^3}{3}}-9x+C=\)

   \(=\displaystyle{\frac{2x^6}{3}}+\displaystyle{\frac{3x^5}{5}}-\displaystyle{\frac{x^4}{2}}+2x^3-9x+C\)

5. Aplicando la linealidad de la integral:

   \(\displaystyle{\int{\left(ax^2+bx+c\right)dx}}=\displaystyle{a\int{x^2dx}}+\displaystyle{b\int{xdx}}+\displaystyle{c\int{1dx}}=\)

   \(=\displaystyle{a \cdot \frac{x^3}{3}}+\displaystyle{b \cdot \frac{x^2}{2}}+cx+C=\displaystyle{\frac{ax^3}{3}}+\displaystyle{\frac{bx^2}{2}}+cx+C\)

Obtén las siguientes integrales indefinidas:

1. \(\displaystyle{\int{\left(x^2-e^{x}\right)dx}}\)
2. \(\displaystyle{\int{\left(\frac{2}{x^4}-x^4\right)dx}}\)
3. \(\displaystyle{\int{\left(1-\frac{3}{x^5}\right)dx}}\)
4. \(\displaystyle{\int{\left(x-\frac{2}{x}\right)dx}}\)
5. \(\displaystyle{\int{\left(3x-2sen(x)\right)dx}}\)
6. \(\displaystyle{\int{\left(3e^x-cos(x)\right)dx}}\)

1. \(\displaystyle{\int{\left(x^2-e^{x}\right)dx}}=\displaystyle{\int{x^2dx}}-\displaystyle{\int{e^{x}dx}}=\displaystyle{\frac{x^3}{3}}-e^{x}+C\)

2. \(\displaystyle{\int{\left(\frac{2}{x^4}-x^4\right)dx}}=\displaystyle{2\int{x^{-4}dx}}-\displaystyle{\int{x^4dx}}=\displaystyle{2\left(\frac{x^{-4+1}}{-4+1}\right)}-\displaystyle{\left(\frac{x^{4+1}}{4+1}\right)}+C=\)

   \(=\displaystyle{2\left(\frac{x^{-3}}{-3}\right)}-\displaystyle{\frac{x^{5}}{5}}+C=\displaystyle{-\frac{2}{3x^3}}-\displaystyle{\frac{x^{5}}{5}}+C\)

3. \(\displaystyle{\int{\left(1-\frac{3}{x^5}\right)dx}}=\displaystyle{\int{1dx}}-\displaystyle{3\int{x^{-5}dx}}=x-\displaystyle{3\left(\frac{x^{-5+1}}{-5+1}\right)}+C=\)

   \(=x-\displaystyle{3\left(\frac{x^{-4}}{-4}\right)}+C=x+\displaystyle{\frac{3}{4x^4}}+C\)

4. \(\displaystyle{\int{\left(x-\frac{2}{x}\right)dx}}=\displaystyle{\int{xdx}}-2\displaystyle{\int{\frac{1}{x}dx}}=\displaystyle{\frac{x^{2}}{2}}-2Ln\left|x\right|+C\)

5. \(\displaystyle{\int{\left(3x-2sen(x)\right)dx}}=\displaystyle{3\int{xdx}}-\displaystyle{2\int{sen(x)dx}}=\displaystyle{3 \cdot \frac{x^{2}}{2}}-2(-cos(x))+C=\)

   \(=\displaystyle{\frac{3x^{2}}{2}}+2cos(x)+C\)

6. \(\displaystyle{\int{\left(3e^x-cos(x)\right)dx}}=3\displaystyle{\int{e^{x}dx}}-\displaystyle{\int{cos(x)dx}}=3e^{x}-sen(x)+C\)

Descomponiendo en sumandos las fracciones obtén:

1. \(\displaystyle{\int{\frac{x-3}{x}dx}}\)
2. \(\displaystyle{\int{\frac{x^2-5x+1}{x}dx}}\)
3. \(\displaystyle{\int{\frac{x^2-3x+1}{x^2}dx}}\)
4. \(\displaystyle{\int{\frac{x^3-3x^2+x-5}{2x^3}dx}}\)
5. \(\displaystyle{\int{\frac{\sqrt[]{x}-2x}{x^2}dx}}\)
6. \(\displaystyle{\int{\frac{3x}{x+4}dx}}\)

1. \(\displaystyle{\int{\frac{x-3}{x}dx}}=\displaystyle{\int{\left(1-\frac{3}{x}\right)dx}}=\displaystyle{\int{1dx}}+\displaystyle{\int{\frac{3}{x}dx}}=\)

   \(=\displaystyle{\int{1dx}}+\displaystyle{3\int{\frac{1}{x}dx}}=x+3Ln\left|x\right|+C\)

2. \(\displaystyle{\int{\frac{x^2-5x+1}{x}dx}}=\displaystyle{\int{\left(x-5+\frac{1}{x}\right)dx}}=\displaystyle{\int{xdx}}-\displaystyle{\int{5dx}}+\displaystyle{\int{\frac{1}{x}dx}}=\)

   \(=\displaystyle{\int{xdx}}-\displaystyle{5\int{1dx}}+\displaystyle{\int{\frac{1}{x}dx}}=\displaystyle{\frac{x^2}{2}}-5x+Ln\left|x\right|+C\)

3. \(\displaystyle{\int{\frac{x^2-3x+1}{x^2}dx}}=\displaystyle{\int{\left(1-\frac{3}{x}+\frac{1}{x^2}\right)dx}}=\displaystyle{\int{1dx}}-\displaystyle{\int{\frac{3}{x}dx}}+\displaystyle{\int{\frac{1}{x^2}dx}}=\)

   \(=\displaystyle{\int{1dx}}-\displaystyle{3\int{\frac{1}{x}dx}}+\displaystyle{\int{x^{-2}dx}}=x-3Ln\left|x\right|+\displaystyle{\frac{x^{-2+1}}{-2+1}}+C=\)

   \(=x-3Ln\left|x\right|+\displaystyle{\frac{x^{-1}}{-1}}+C=x-3Ln\left|x\right|-\displaystyle{\frac{1}{x}}+C\)

4. \(\displaystyle{\int{\frac{x^3-3x^2+x-5}{2x^3}dx}}=\displaystyle{\int{\frac{1}{2}dx}}-\displaystyle{\int{\frac{3}{2x}dx}}+\displaystyle{\int{\frac{1}{2x^2}dx}}-\displaystyle{\int{\frac{5}{2x^3}dx}}=\)

   \(=\displaystyle{\frac{1}{2}}\displaystyle{\int{1dx}}-\displaystyle{\frac{3}{2}}\displaystyle{\int{\frac{1}{x}dx}}+\displaystyle{\frac{1}{2}}\displaystyle{\int{\frac{1}{x^2}dx}}-\displaystyle{\frac{5}{2}}\displaystyle{\int{\frac{1}{x^3}dx}}=\)

   \(=\displaystyle{\frac{1}{2}}\displaystyle{\int{1dx}}-\displaystyle{\frac{3}{2}}\displaystyle{\int{\frac{1}{x}dx}}+\displaystyle{\frac{1}{2}}\displaystyle{\int{x^{-2}dx}}-\displaystyle{\frac{5}{2}}\displaystyle{\int{x^{-3}dx}}=\)

   \(=\displaystyle{\frac{1}{2}}x-\displaystyle{\frac{3}{2}}Ln\left|x\right|+\displaystyle{\frac{1}{2}}\displaystyle{\left(\frac{x^{-2+1}}{-2+1}\right)}-\displaystyle{\frac{5}{2}}\displaystyle{\left(\frac{x^{-3+1}}{-3+1}\right)}+C=\)

   \(=\displaystyle{\frac{1}{2}}x-\displaystyle{\frac{3}{2}}Ln\left|x\right|+\displaystyle{\frac{1}{2}}\displaystyle{\left(\frac{x^{-1}}{-1}\right)}-\displaystyle{\frac{5}{2}}\displaystyle{\left(\frac{x^{-2}}{-2}\right)}+C=\)

   \(=\displaystyle{\frac{1}{2}}x-\displaystyle{\frac{3}{2}}Ln\left|x\right|+\displaystyle{\frac{1}{2}}\displaystyle{\left(\frac{-1}{x}\right)}-\displaystyle{\frac{5}{2}}\displaystyle{\left(\frac{-1}{2x^{2}}\right)}+C=\)

   \(=\displaystyle{\frac{1}{2}}x-\displaystyle{\frac{3}{2}}Ln\left|x\right|+\displaystyle{\left(\frac{-1}{2x}\right)}-\displaystyle{\left(\frac{-5}{4x^{2}}\right)}+C=\displaystyle{\frac{1}{2}}x-\displaystyle{\frac{3}{2}}Ln\left|x\right|-\displaystyle{\frac{1}{2x}}+\displaystyle{\frac{5}{4x^{2}}}+C\)

5. \(\displaystyle{\int{\frac{\sqrt[]{x}-2x}{x^2}dx}}=\displaystyle{\int{\frac{\sqrt[]{x}}{x^2}dx}}-\displaystyle{2\int{\frac{x}{x^2}dx}}=\displaystyle{\int{\frac{x^{\frac{1}{2}}}{x^2}dx}}-\displaystyle{2\int{\frac{1}{x}dx}}=\)

   \(=\displaystyle{\int{x^{-\frac{3}{2}}dx}}-\displaystyle{2\int{\frac{1}{x}dx}}=\displaystyle{\frac{x^{-\frac{3}{2}+1}}{-\frac{3}{2}+1}}-2Ln\left|x\right|+C=\displaystyle{\frac{x^{-\frac{1}{2}}}{-\frac{1}{2}}}-2Ln\left|x\right|+C=\)

   \(=-\displaystyle{\frac{2}{x^{\frac{1}{2}}}}-2Ln\left|x\right|+C=-\displaystyle{\frac{2}{\sqrt[]{x}}}-2Ln\left|x\right|+C\)

6. \(\displaystyle{\int{\frac{3x}{x+4}dx}}=\displaystyle{3\int{\frac{(x-4)-4}{x+4}dx}}=\displaystyle{3\int{\frac{x-4}{x+4}dx}}+\displaystyle{3\int{\frac{-4}{x+4}dx}}=\)

   \(=\displaystyle{3\int{1dx}}-\displaystyle{12\int{\frac{1}{x+4}dx}}= \left\{\begin{array}{l} u=x-4\\ du=1dx\\ \end{array}\right\} =3x-\displaystyle{12\int{\frac{du}{u}}}=\)

   \(=3x-12Ln\left|u\right|+C=3x-12Ln\left|x-4\right|+C\)

Obtén las siguientes integrales logarítmicas:

1. \(\displaystyle{\int{\frac{1}{x-2}dx}}\)
2. \(\displaystyle{\int{\frac{x^2}{x^3-8}dx}}\)
3. \(\displaystyle{\int{\frac{e^{x}-2x}{e^{x}-x^2+5}dx}}\)
4. \(\displaystyle{\int{\frac{cos(x)-sen(x)}{sen(x)+cos(x)}dx}}\)

1. \(\displaystyle{\int{\frac{1}{x-2}dx}}= \left\{\begin{array}{l} u=x-2\\ du=1dx\\ \end{array}\right\} =\displaystyle{\int{\frac{1}{u}du}}=Ln\left|u\right|+c=Ln\left|x-2\right|+C\)
2. \(\displaystyle{\int{\frac{x^2}{x^3-8}dx}}= \left\{\begin{array}{l} u=x^3-8\\ du=3x^2dx\\ \end{array}\right\} =\displaystyle{\int{\frac{3}{3} \cdot \frac{x^2}{x^3-8}dx}}=\displaystyle{\int{\frac{1}{3} \cdot \frac{du}{u}}}=\frac{1}{3}\displaystyle{\int{\frac{du}{u}}}=\displaystyle{\frac{1}{3}}Ln\left|u\right|+c=\displaystyle{\frac{1}{3}}Ln\left|x^3-8\right|+C\)
3. \(\displaystyle{\int{\frac{e^{x}-2x}{e^{x}-x^2+5}dx}}= \left\{\begin{array}{l} u=e^{x}-x^2+5\\ du=\left(e^{x}-2x\right)dx\\ \end{array}\right\} =\displaystyle{\int{\frac{du}{u}}}=Ln\left|u\right|+c=Ln\left|e^{x}-x^2+5\right|+C\)
4. \(\displaystyle{\int{\frac{cos(x)-sen(x)}{sen(x)+cos(x)}dx}}= \left\{\begin{array}{l} u=sen(x)+cos(x)\\ du=\left(cos(x)-sen(x)\right)dx\\ \end{array}\right\} =\displaystyle{\int{\frac{du}{u}}}=Ln\left|u\right|+c=Ln\left|sen(x)+cos(x)\right|+C\)

Obtén las siguientes integrales de formas compuestas relacionadas con la función exponencial:

1. \(\displaystyle{\int{e^{3x-2}dx}}\)
2. \(\displaystyle{\int{3x^2 e^{x^3-4}dx}}\)
3. \(\displaystyle{\int{e^{cos(x)}sen(x)dx}}\)
4. \(\displaystyle{\int{(2x-1) e^{x^2-x}dx}}\)

1. \(\displaystyle{\int{e^{3x-2}dx}}= \left\{\begin{array}{l} u=3x-2\\ du=3dx\\ \end{array}\right\} =\displaystyle{\int{\frac{3}{3} \cdot e^{3x-2}dx}}=\displaystyle{\int{\frac{1}{3} \cdot e^{u}du}}=\frac{1}{3}\displaystyle{\int{e^{u}du}}=\frac{1}{3}e^{u}+C=\frac{1}{3}e^{3x-2}+C\)
2. \(\displaystyle{\int{3x^2 e^{x^3-4}dx}}= \left\{\begin{array}{l} u=x^3-4\\ du=3x^2dx\\ \end{array}\right\} =\displaystyle{\int{e^{u}du}}=e^{u}+C=e^{x^3-4}+C\)
3. \(\displaystyle{\int{e^{cos(x)}sen(x)dx}}= \left\{\begin{array}{l} u=cos(x)\\ du=-sen(x)dx\\ \end{array}\right\} =\displaystyle{-\int{-e^{cos(x)}sen(x)dx}}=\displaystyle{-\int{e^{u}du}}=-e^{u}+C=-e^{cos(x)}+C\)
4. \(\displaystyle{\int{(2x-1) e^{x^2-x}dx}}= \left\{\begin{array}{l} u=x^2-x\\ du=\left(2x-1\right)dx\\ \end{array}\right\} =\displaystyle{\int{e^{u}du}}=e^{u}+C=e^{x^2-x}+C\)

Obtén las siguientes integrales de formas compuestas de forma potencial:

1. \(\displaystyle{\int{(3x-2)^3dx}}\)
2. \(\displaystyle{\int{6x(3x^2-2)^5dx}}\)
3. \(\displaystyle{\int{x\sqrt[3]{x^2-1}dx}}\)
4. \(\displaystyle{\int{sen^3(x)cos(x)dx}}\)

1. \(\displaystyle{\int{(3x-2)^3dx}}= \left\{\begin{array}{l} u=3x-2\\ du=3dx\\ \end{array}\right\} =\displaystyle{\int{\frac{3}{3} \cdot (3x-2)^3dx}}=\displaystyle{\int{\frac{1}{3} \cdot u^3du}}=\displaystyle{\frac{1}{3}} \displaystyle{\int{u^3du}} =\displaystyle{\frac{1}{3}} \displaystyle{\frac{u^4}{4}}+C=\displaystyle{\frac{1}{3}} \displaystyle{\frac{(3x-2)^4}{4}}+C\)
2. \(\displaystyle{\int{6x(3x^2-2)^5dx}}= \left\{\begin{array}{l} u=3x^2-2\\ du=6xdx\\ \end{array}\right\} =\displaystyle{\int{u^5du}}=\displaystyle{\frac{u^6}{6}}+C=\displaystyle{\frac{(3x^2-2)^6}{6}}+C\)
3. \(\displaystyle{\int{x\sqrt[3]{x^2-1}dx}}= \left\{\begin{array}{l} u=x^2-1\\ du=2xdx\\ \end{array}\right\} =\displaystyle{\int{\frac{2}{2} \cdot x\sqrt[3]{x^2-1}dx}}=\displaystyle{\int{\frac{1}{2} \cdot \sqrt[3]{u}du}}=\displaystyle{\frac{1}{2}} \displaystyle{\int{\sqrt[3]{u}du}} =\displaystyle{\frac{1}{2}} \displaystyle{\int{u^{\frac{1}{3}}du}}=\displaystyle{\frac{1}{2}} \displaystyle{\frac{u^{\frac{1}{3}+1}}{\frac{1}{3}+1}}+C=\) \(=\displaystyle{\frac{1}{2}} \displaystyle{\frac{u^{\frac{4}{3}}}{\frac{4}{3}}}+C=\displaystyle{\frac{1}{2}} \displaystyle{\frac{3\sqrt[3]{u^4}}{4}}+C=\displaystyle{\frac{3\sqrt[3]{u^4}}{8}}+C=\displaystyle{\frac{3u\sqrt[3]{u}}{8}}+C=\displaystyle{\frac{3\left(x^2-1\right)\sqrt[3]{x^2-1}}{8}}+C\)
4. \(\displaystyle{\int{sen^3(x)cos(x)dx}}= \left\{\begin{array}{l} u=sen(x)\\ du=cos(x)dx\\ \end{array}\right\} =\displaystyle{\int{u^3du}}=\displaystyle{\frac{u^4}{4}}+C=\displaystyle{\frac{sen^4(x)}{4}}+C\)

Obtén las siguientes integrales de formas compuestas de forma potencial:

1. \(\displaystyle{\int{cos(2x-1)dx}}\)
2. \(\displaystyle{\int{xcos(x^2+1)dx}}\)
3. \(\displaystyle{\int{3x^4sen(x^5)dx}}\)
4. \(\displaystyle{\int{sen(10x)dx}}\)

1. \(\displaystyle{\int{cos(2x-1)dx}}= \left\{\begin{array}{l} u=2x-1\\ du=2dx\\ \end{array}\right\} =\displaystyle{\int{\frac{2}{2}cos(2x-1)dx}}=\displaystyle{\int{\frac{1}{2}cos(u)du}}=\) \(=\displaystyle{\frac{1}{2}}\displaystyle{\int{cos(u)du}}=\displaystyle{\frac{1}{2}}sen(u)+C=\displaystyle{\frac{1}{2}}sen(2x-1)+C\)
2. \(\displaystyle{\int{xcos(x^2+1)dx}}= \left\{\begin{array}{l} u=x^2+1\\ du=2dx\\ \end{array}\right\} =\displaystyle{\int{\frac{2}{2}cos(x^2+1)dx}}=\displaystyle{\int{\frac{1}{2}cos(u)du}}=\) \(=\displaystyle{\frac{1}{2}}\displaystyle{\int{cos(u)du}}=\displaystyle{\frac{1}{2}}sen(u)+C=\displaystyle{\frac{1}{2}}sen(x^2+1)+C\)
3. \(\displaystyle{\int{3x^4sen(x^5)dx}}= \left\{\begin{array}{l} u=x^5\\ du=5x^4dx\\ \end{array}\right\} =\displaystyle{\int{\frac{5}{5}3x^4sen(x^5)dx}}=\displaystyle{\int{\frac{3}{5}sen(u)du}}=\) \(=\displaystyle{\frac{3}{5}}\displaystyle{\int{sen(u)du}}=\displaystyle{\frac{3}{5}}\left(-cos(u)\right)+C=-\frac{3}{5}cos(x^5)+C\)
4. \(\displaystyle{\int{sen(10x)dx}}= \left\{\begin{array}{l} u=10x\\ du=10dx\\ \end{array}\right\} =\displaystyle{\int{\frac{10}{10}sen(10x)dx}}=\displaystyle{\int{\frac{1}{10}sen(u)du}}=\) \(=\displaystyle{\frac{1}{10}}\displaystyle{\int{sen(u)du}}=\displaystyle{\frac{1}{10}}\left(-cos(u)\right)+C=-\frac{1}{10}cos(10x)+C\)

Halla la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) sabiendo \(f''(x)=12x-6\) y que la recta tangente a la gráfica de \(f\) en el punto de abscisa \(x=2\) tiene de ecuación \(4x-y-7=0\).

Aplicando la linealidad de la integral:

\(f'(x)=\displaystyle{\int{f''(x)dx}}=\displaystyle{\int{(12x-6)dx}}=\displaystyle{12\int{xdx}}-\displaystyle{6\int{1dx}}=\displaystyle{12 \cdot \frac{x^2}{2}}-6x+C_1=6x^2-6x+C_1\)

\(f(x)=\displaystyle{\int{f'(x)dx}}=\displaystyle{\int{\left(6x^2-6x+C_1\right)dx}}=\displaystyle{6\int{x^2dx}}-\displaystyle{6\int{xdx}}+\displaystyle{C_1\int{1dx}}=\)

\(=\displaystyle{6 \cdot \frac{x^3}{3}}-\displaystyle{6 \cdot \frac{x^2}{2}}+\displaystyle{C_1x}+C_2=\displaystyle{2x^3}-\displaystyle{3x^2}+\displaystyle{C_1x}+C_2\)

Si para \(x=2\) la recta tangente es \(4x-y-7=0 \Rightarrow y=4x-7 \Rightarrow m=4\)

La coordenada \(y\) del punto de tangencia la obtenemos sustituyendo en la ecuación de la recta tangente:

Si \(x=2 \Rightarrow y=4 \cdot 2-7=1 \Rightarrow P(2,1)\)

Por el punto de tangencia ambas gráficas pasan, por tanto: \(\left\{\begin{array}{l} f(2)=1\\ f'(2)=4\\ \end{array}\right.\)

Por tanto, sustituyendo en \(f(x)\) se obtiene que:

\(f(2)=1 \Rightarrow \displaystyle{2 \cdot 2^3}-\displaystyle{3 \cdot 2^2}+\displaystyle{C_1 \cdot 2}+C_2=1 \Rightarrow 16-12+2C_1+C_2=1 \Rightarrow 2C_1+C_2=-3\) \((*)\)

Y sustituyendo en \(f'(x)\) se obtiene que:

\(f'(2)=4 \Rightarrow 6 \cdot 2^2-6 \cdot 2+C_1=4 \Rightarrow 24-12+C_1=4 \Rightarrow C_1=-8 \)

Y sustituyendo en \((*)\) se obtiene que: \(2(-8)+C_2=-3 \Rightarrow C_2=13\)

Por tanto, \(f(x)=\displaystyle{2x^3}-\displaystyle{3x^2}-\displaystyle{8x}+13\)

Calcula:

1. \(\displaystyle{\int_{0}^{2}{(x^2+x-2)dx}}\)
2. \(\displaystyle{\int_{-1}^{1}{(x^2-1)dx}}\)
3. \(\displaystyle{\int_{1}^{2}{\frac{3}{x+2}dx}}\)
4. \(\displaystyle{\int_{0}^{1}{xe^{x^2}dx}}\)

1. Calculamos la integral indefinida: \(F(x)=\displaystyle{\int{(x^2+x-2)dx}}=\displaystyle{\frac{x^3}{3}+\frac{x^2}{2}-2x}+C\)

   Aplicamos la regla de Barrow: \(f(x)=x^2+x-2\) continua en \([0,2]\)

   \(\displaystyle{\int_{0}^{2}{(x^2+x-2)dx}}={\left[F(x)\right]}_{x=0}^{x=2}=F(2)-F(0)=\left(\displaystyle{\frac{2^3}{3}+\frac{2^2}{2}-2 \cdot 2}+C\right)-\left(\displaystyle{\frac{0^3}{3}+\frac{0^2}{2}-2 \cdot 0}+C\right)=\)

   \(=\left(\displaystyle{\frac{8}{3}+2-4}+C\right)-\left(\displaystyle{0}+C\right)=\displaystyle{\frac{8}{3}-2}+C-C=\displaystyle{\frac{2}{3}}\)

2. Calculamos la integral indefinida: \(F(x)=\displaystyle{\int{(x^2-1)dx}}=\displaystyle{\frac{x^3}{3}-x}+C\)

   Aplicamos la regla de Barrow: \(f(x)=x^2-1\) continua en \([-1,1]\)

   \(\displaystyle{\int_{-1}^{1}{(x^2-1)dx}}={\left[F(x)\right]}_{x=1}^{x=-1}=F(1)-F(-1)=\left(\displaystyle{\frac{1^3}{3}-1}+C\right)-\left(\displaystyle{\frac{(-1)^3}{3}-(-1)}+C\right)=\)

   \(=\left(\displaystyle{\frac{1}{3}-1}+C\right)-\left(\displaystyle{\frac{1}{3}+1}+C\right)=\displaystyle{-\frac{2}{3}}+C-\displaystyle{\frac{4}{3}}-C=-2\)

3. Calculamos la integral indefinida: \(F(x)=\displaystyle{\int{\frac{3}{x+2}dx}}=3Ln\left|x+2\right|+C\)

   Aplicamos la regla de Barrow: \(f(x)=\displaystyle{\frac{3}{x+2}}\) continua en \([1,2]\)

   \(\displaystyle{\int_{1}^{2}{\frac{3}{x+2}dx}}={\left[F(x)\right]}_{x=1}^{x=2}=F(2)-F(1)=\left(3Ln\left|2+2\right|+C\right)-\left(3Ln\left|1+2\right|+C\right)=\)

   \(=3Ln\left|4\right|+C-3Ln\left|3\right|-C=3Ln(4)-3Ln(3)=Ln(4^3)-Ln(3^3)=Ln\left(\displaystyle{\frac{64}{27}}\right)\)

4. Calculamos la integral indefinida: \(F(x)=\displaystyle{\int{xe^{x^2}dx}}=\displaystyle{\frac{e^{x^2}}{2}}+C\)

   Aplicamos la regla de Barrow: \(f(x)=xe^{x^2}\) continua en \([0,1]\)

   \(\displaystyle{\int_{0}^{1}{xe^{x^2}dx}}={\left[F(x)\right]}_{x=0}^{x=1}=F(1)-F(0)=\left(\displaystyle{\frac{e^{1^2}}{2}}+C\right)-\left(\displaystyle{\frac{e^{0^2}}{2}}+C\right)=\left(\displaystyle{\frac{e^{1}}{2}}+C\right)-\left(\displaystyle{\frac{e^{0}}{2}}+C\right)=\)

   \(=\left(\displaystyle{\frac{e}{2}}+C\right)-\left(\displaystyle{\frac{1}{2}}+C\right)=\displaystyle{\frac{e}{2}}+C-\displaystyle{\frac{1}{2}}-C=\displaystyle{\frac{e}{2}}-\displaystyle{\frac{1}{2}}=\displaystyle{\frac{e-1}{2}}\)

Calcula el área delimitada por la curva \(y=x^3-4x\) con el eje de abscisas en el intervalo \([-1,3]\).

Resolviendo la ecuación \(f(x)=0\) obtenemos:

\(f(x)=0 \Rightarrow x^3-4x=0 \Rightarrow x(x^2-4)=0 \Rightarrow \left\{\begin{array}{c} x=0\\ ó\\ x^2-4=0\\ \end{array}\right. \Rightarrow \left\{\begin{array}{c} x=0\\ ó\\ x^2=4\\ \end{array}\right. \Rightarrow \left\{\begin{array}{c} x=0\\ ó\\ x=-2\\ ó\\ x=+2\\ \end{array}\right. \)

Haciendo un esbozo de la gráfica de la función, mediante una tabla de valores y calculando los límites en \(\pm \infty\), se deduce que:

$$\left\{\begin{array}{c} \displaystyle{\lim_{x \rightarrow -\infty}{x^3-4x}}=-\infty\\ \displaystyle{\lim_{x \rightarrow +\infty}{x^3-4x}}=+\infty\\ \end{array}\right.$$

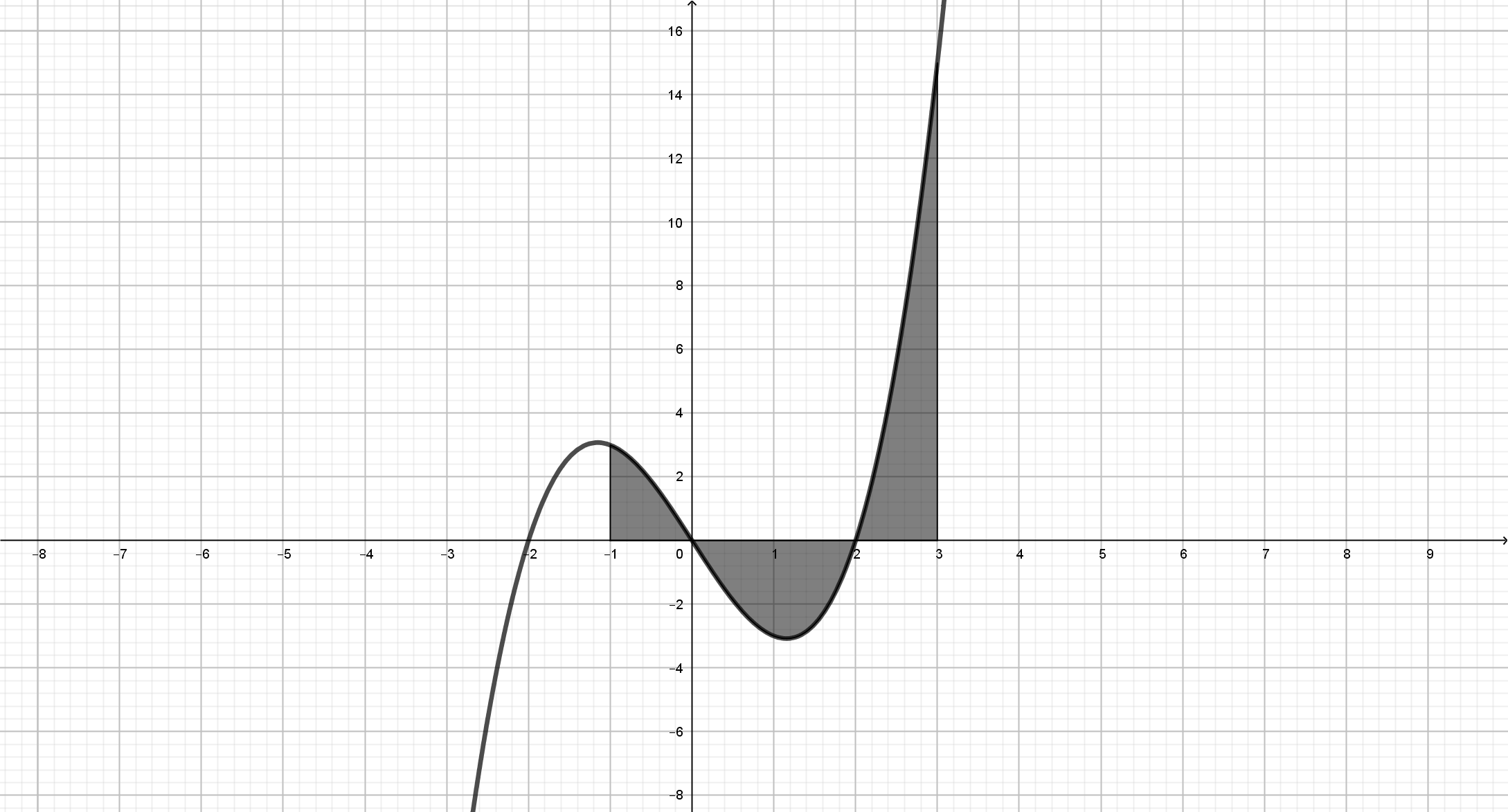
$$Área(\mathbf{R})=Área(\mathbf{R_1})+Área(\mathbf{R_2})+Área(\mathbf{R_3})$$

Calculamos la integral indefinida y aplicando la regla de Barrow en cada una de las regiones:

$$F(x)=\displaystyle{\int{\left(x^3-4x\right)dx}}=\displaystyle{\frac{x^4}{4}}-2x^2+C$$

\(Área(\mathbf{R_1})=\displaystyle{\int_{-1}^{0}{\left(x^3-4x\right)dx}}=\left[F(x)\right]_{x=-1}^{x=0}=\left(\displaystyle{\frac{0^4}{4}}-2 \cdot 0^2+C\right)-\left(\displaystyle{\frac{(-1)^4}{4}}-2\cdot (-1)^2+C\right)=\displaystyle{\frac{7}{4}}\)

\(Área(\mathbf{R_2})=-\displaystyle{\int_{0}^{2}{\left(x^3-4x\right)dx}}=-\left[F(x)\right]_{x=0}^{x=2}=-\left(\left(\displaystyle{\frac{2^4}{4}}-2 \cdot 2^2+C\right)-\left(\displaystyle{\frac{0^4}{4}}-2 \cdot 0^2+C\right)\right)=-\left(-4\right)=4\)

\(Área(\mathbf{R_3})=\displaystyle{\int_{2}^{3}{\left(x^3-4x\right)dx}}=\left[F(x)\right]_{x=2}^{x=3}=\left(\displaystyle{\frac{3^4}{4}}-2 \cdot 3^2+C\right)-\left(\displaystyle{\frac{2^4}{4}}-2 \cdot 2^2+C\right)=\displaystyle{\frac{25}{4}}\)

$$Área(\mathbf{R})=Área(\mathbf{R_1})+Área(\mathbf{R_2})+Área(\mathbf{R_3})=\displaystyle{\frac{7}{4}}+4+\displaystyle{\frac{7}{4}}=12$$

Algunos resultados teóricos

Interpretación geométrica de la integral definida de una función en un intervalo cerrado

La integral definida coincide con el área sólo cuando la función es positiva, es decir, está por encima del \(\hbox{eje X}\). Cuando la función en negativa, la integral también es negativa, dándonos el área cambiada de signo. Y cuando la función cambia de signo, es decir, está por encima y por debajo del \(\hbox{eje X}\), la integral es igual a la resta entre las áreas de las regiones superiores y las áreas de las regiones inferiores.

Área encerrada entre una curva y el eje X

• Resolvemos la ecuación \(f(x)=0\). Supongamos que los ceros obtenidos en el intervalo \([a,b]\), ordenados de menor a mayor, son \(x=x_1,x_2,\cdots,x_n.\)

• Calculamos las integrales: \(\displaystyle{\int_{a}^{x_1}{f(x)dx}},\displaystyle{\int_{x_1}^{x_2}{f(x)dx}}, \cdots, \displaystyle{\int_{x_n}^{b}{f(x)dx}}.\)

• El área es la suma de los valores absolutos de cada una de las integrales anteriores.

Área encerrada entre dos curvas

Dadas las funciones \(f(x)\) y \(g(x)\), \(f(x) \geq g(x)\), para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):

• Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a\) y \(x=b\).

• Calculamos la integral: \(\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}\).

  Aplicando la linealidad de la integral y teniendo en cuenta que \(\displaystyle{\int_{a}^{b}{f(x)dx}}=Área(\mathbf{R_1})\) y \(\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_2})\):

  $$Área(\mathbf{R})=\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}=\displaystyle{\int_{a}^{b}{f(x)dx}}-\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_1})-Área(\mathbf{R_2})$$

En general, para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):

• Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a,x=c\) y \(x=b\).

• Calculamos las integrales: \(\displaystyle{\int_{a}^{c}{\left(f(x)-g(x)\right)dx}}\) y \(\displaystyle{\int_{c}^{b}{\left(f(x)-g(x)\right)dx}}\).

• El área es la suma de los valores absolutos de las integrales anteriores (de ese modo no hay que tener en cuenta qué función es mayor y menor en cada intervalo).
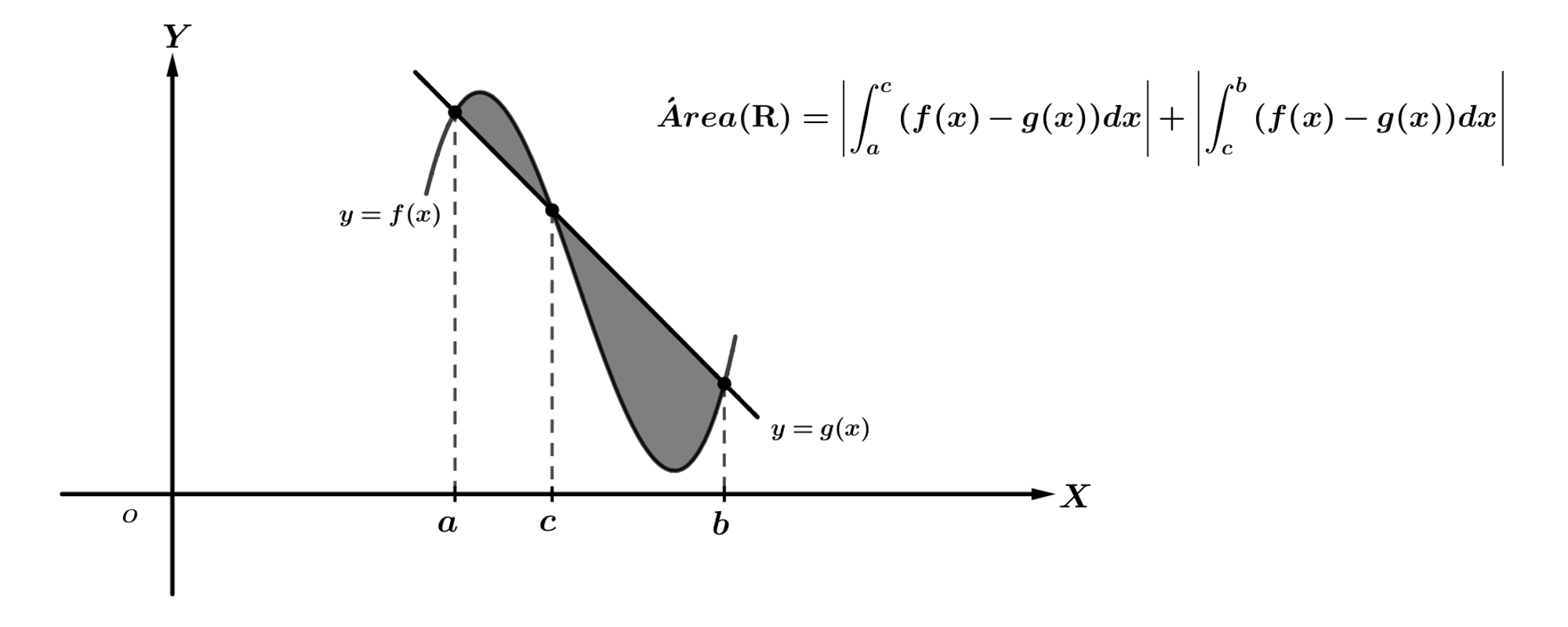