¿Cuál es el valor de \(\displaystyle{\int_{1}^{2}{\left(3x^2-4\right)}dx}\)?

$$ \left.\begin{array}{llll} a)-5 & b)3 & c)-19 & d)-3 \\ \end{array}\right. $$

\(b)3\)

Dada la función \(f(x)=x^2-1\) en el intervalo \([0,1]\), ¿cuál es el valor de \(\displaystyle{\int_{0}^{1}{f(x)}dx}\)?

$$ \left.\begin{array}{llll} a)0 & b)\displaystyle{\frac{2}{3}} & c)\displaystyle{\frac{4}{3}} & d)\displaystyle{-\frac{2}{3}} \\ \end{array}\right. $$

\(d)\displaystyle{-\frac{2}{3}}\)

Dada la función \(f(x)=x^2-1\) en el intervalo \([1,2]\), ¿cuál es el valor de \(\displaystyle{\int_{1}^{2}{f(x)}dx}\)?

$$ \left.\begin{array}{llll} a)\displaystyle{-\frac{2}{3}} & b)2 & c)\displaystyle{\frac{2}{3}} & d)\displaystyle{\frac{4}{3}} \\ \end{array}\right. $$

\(d)\displaystyle{\frac{4}{3}}\)

¿Cuál es el área del recinto limitado por la función \(f(x)=x^2-1\) y el eje \(X\) en el intervalo \([0,2]\)?

$$ \left.\begin{array}{llll} a)\displaystyle{\frac{2}{3}} & b)2 & c)\displaystyle{-\frac{2}{3}} & d)0 \\ \end{array}\right. $$

\(a)\displaystyle{\frac{2}{3}}\)

Dadas las funciones \(f(x)=x^2-4x\) y \(g(x)=x-4\),

¿Cuáles son sus puntos de corte?

$$ \left.\begin{array}{l} a)A(-3,1), B(4,0)\\ b)A(0,0), B(4,0)\\ c)A(1,-3), B(4,0)\\ d)A(1,-3), B(0,4)\\ \end{array}\right. $$

\(c)A(1,-3), B(4,0)\)

Dadas las funciones \(f(x)=x^2-4x\) y \(g(x)=x-4\),

el área del recinto limitado por ambas curvas se obtiene directamente calculando:

$$ \left.\begin{array}{l} a)\displaystyle{\int_{1}^{4}{\left(f(x)-g(x)\right)dx}}\\ b)\displaystyle{\int_{1}^{4}{\left(g(x)-f(x)\right)dx}}\\ c)\displaystyle{\int_{-3}^{0}{\left(f(x)-g(x)\right)dx}}\\ d)\displaystyle{\int_{0}^{4}{\left(g(x)-f(x)\right)dx}}\\ \end{array}\right. $$

\(b)\displaystyle{\int_{1}^{4}{\left(g(x)-f(x)\right)dx}}\)

Dadas las funciones \(f(x)=x^2-4x\) y \(g(x)=x-4\),

el área del recinto limitado por ambas curvas vale:

$$ \left.\begin{array}{llll} a)\displaystyle{-\frac{9}{2}} & b)\displaystyle{\frac{3}{2}} & c)\displaystyle{\frac{111}{2}} & d)\displaystyle{\frac{9}{2}}\\ \end{array}\right. $$

\(d)\displaystyle{\frac{9}{2}}\)

A la vista del siguiente gráfico, se deduce que el área limitada por ambas curvas es:

a)Positiva, ya que un área siempre es positiva

b)Negativa, porque el recinto está por debajo del eje \(X\)

c)Negativa, porque \(f(x)\) está por encima de \(g(x)\)

d)Negativa, porque \(g(x)\) está por encima de \(f(x)\)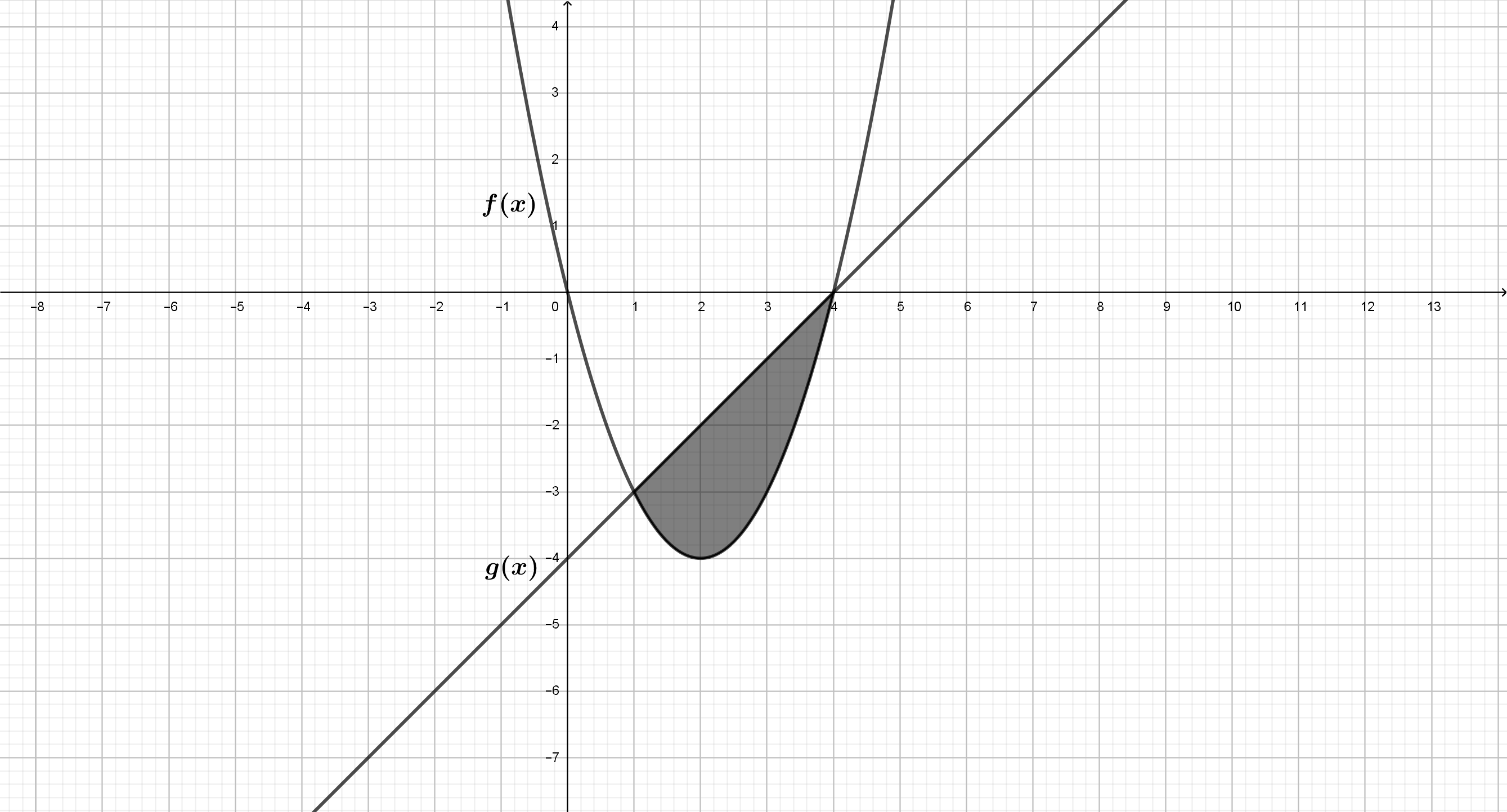

a)Positiva, ya que un área siempre es positiva

Algunos resultados teóricos