Aula MatemáTICa, tu blog de aula...

Probabilidad

Sucesos y operaciones con sucesos

$$\left\{\begin{array}{c} \mathbf{\hbox{(Suceso seguro) }} X \\ \\ \mathbf{\hbox{(Suceso imposible) }} \varnothing \\ \\ \mathbf{\hbox{ (Intersección de sucesos) }} A \cap B = \begin{Bmatrix} x / x \in A \wedge x \in B \end{Bmatrix}\\ \\ \mathbf{\hbox{ (Unión de sucesos) }} A \cup B = \begin{Bmatrix} x / x \in A \vee x \in B \end{Bmatrix}\\ \\ \mathbf{\hbox{ (Diferencia de sucesos) }} A - B = \begin{Bmatrix} x / x \in A \wedge x \notin B \end{Bmatrix} = A \cap \overline{B}\\ \\ \mathbf{\hbox{ (Contrario o complementario de un suceso) }} \left\{\begin{array}{l} \overline{A} = \begin{Bmatrix} x / x \notin A \end{Bmatrix}\\ \\ \left.\begin{array}{l} \overline{A} = X - A\\ \overline{\overline{A}} = A\\ X = A \cup \overline{A}\\ A = (A \cap B) \cup (A \cap \overline{B})\\ \end{array}\right.\\ \end{array}\right.\\ \\ \mathbf{\hbox{(Leyes de Morgan)}} \left\{\begin{array}{l} \overline{A \cup B} = \overline{A} \cap \overline{B}\\ \overline{A \cap B} = \overline{A} \cup \overline{B}\\ \end{array}\right.\\ \\ \mathbf{\hbox{ (Incompatibilidad de sucesos) }} \hbox{A y B son incompatibles} \Leftrightarrow A \cap B = \varnothing\\ \end{array}\right. $$

Cálculo de Probabilidades

$$\left\{\begin{array}{c} \left.\begin{array}{c} P(\varnothing)=0, P(X)=1 \\ \\ \varnothing \subseteq A \subseteq X \Rightarrow 0 \leq P(A) \leq 1\\ \end{array} \right.\\ \\ \mathbf{\hbox{ (Probabilidad de la unión) }} \left\{\begin{array}{l} P(A \cup B) = P(A) + P(B) - P(A \cap B) \\ \\ \hbox{Si A y B incompatibles} \Rightarrow P(A \cup B) = P(A) + P(B) \\ \end{array}\right.\\ \\ \left.\begin{array}{c} \hbox{En general, dados n sucesos } A_1, A_2, \cdots , A_n: \\ \\ P(A_1 \cup \cdots \cup A_n) = \sum_{i=1}^{n}P(A_i) - \sum_{i \neq j}^{}P(A_i \cap A_j) + \sum_{i \neq j \neq k}^{}P(A_i \cap A_j \cap A_k) - \cdots +(-1)^n P(A_1 \cap \cdots \cap A_n)\\ \\ \hbox{Si } \forall i \neq j, A_i \hbox{ y } A_j \hbox{ son incompatibles} \Rightarrow P(A_1 \cup \cdots \cup A_n) = \sum_{k=1}^{n}P(A_k)\\ \end{array}\right.\\ \\ \mathbf{\hbox{ (Probabilidad del contrario) }} P(\overline{A})=1-P(A) \\ \\ \mathbf{\hbox{(Regla de Laplace) }} P(A)=\frac{\hbox{Casos favorables a A}}{\hbox{Casos posibles}} \hbox{ , si todos los sucesos elementales son equiprobables}\\ \end{array}\right.$$

Experiencias compuestas

$$\left\{\begin{array}{l} \mathbf{\hbox{(Probabilidad condicionada) }} P(A|B)=\displaystyle{\frac{P(A \cap B)}{P(B)}} \hbox{ , es la probabilidad de que ocurra A sabiendo que ha ocurrido B}\\ \\ \mathbf{\hbox{(Intersección de sucesos) }} \left\{\begin{array}{l} P(A \cap B)=P(A) \cdot P(B|A)\\ \\ P(A \cap B \cap C)=P(A) \cdot P(B|A) \cdot P(C|A \cap B)\\ \\ P(A_1 \cap \cdots \cap A_n)=P(A_1) \cdot P(A_2|A_1) \cdots P(A_n|A_1 \cap \cdots \cap A_{n-1})\\ \end{array}\right.\\ \\ \mathbf{\hbox{(Independencia de sucesos) }} \hbox{A y B independientes} \Leftrightarrow P(A \cap B)=P(A) \cdot P(B) \Leftrightarrow P(A|B)=P(A) \hbox{ si P(B)} \neq 0\\ \end{array}\right.$$

Sistema completo de sucesos

Un sistema completo de sucesos $S_{1}, S_{2}, \cdots, S_{n}$ es un conjunto de sucesos cuya unión es el total, es decir, es el espacio muestral $X$, e incompatibles dos a dos, es decir, la intersección de cualesquiera dos de ellos es el conjunto vacío.

$$ \left\{\begin{array}{l} S_1 \cup \cdots \cup S_n = X\\ S_i \cap S_j=\varnothing \hbox{ } \forall i,j \end{array}\right.$$

Ejemplo:

Dado un suceso $A$, en todo sistema completo de sucesos se cumple:

$$\left\{\begin{array}{l} \mathbf{\hbox{ (Teorema de la Probabilidad Total) }} P(A)=\displaystyle{\sum_{k=1}^{n}P(S_k)\cdot P(A|S_k)} \\ \\ \mathbf{\hbox{ (Teorema de Bayes) }} P(S_i|A)=\displaystyle{\frac{P(S_i) \cdot P(A|S_i)}{\displaystyle{\sum_{k=1}^{n}P(S_k)\cdot P(A|S_k)}}} \\ \end{array}\right.$$

Ejemplo:

Teorema de la Probabilidad Total:

$$\left\{\begin{array}{l} P(A)=P(S_1) \cdot P(A|S_1)+P(S_2) \cdot P(A|S_2)+P(S_3) \cdot P(A|S_3)+P(S_4) \cdot P(A|S_4)\\ \\ P(\overline{A})=P(S_1) \cdot P(\overline{A}|S_1)+P(S_2) \cdot P(\overline{A}|S_2)+P(S_3) \cdot P(\overline{A}|S_3)+P(S_4) \cdot P(\overline{A}|S_4)\\ \end{array}\right.$$

Teorema de Bayes:

$$\left\{\begin{array}{l} P(S_1|A)=\displaystyle{\frac{P(S_1) \cdot P(A|S_1)}{P(S_1) \cdot P(A|S_1)+P(S_2) \cdot P(A|S_2)+P(S_3) \cdot P(A|S_3)+P(S_4) \cdot P(A|S_4)}}\\ \\ P(S_1|\overline{A})=\displaystyle{\frac{P(S_1) \cdot P(\overline{A}|S_1)}{P(S_1) \cdot P(\overline{A}|S_1)+P(S_2) \cdot P(\overline{A}|S_2)+P(S_3) \cdot P(\overline{A}|S_3)+P(S_4) \cdot P(\overline{A}|S_4)}}\\ \\ P(S_2|A)=\displaystyle{\frac{P(S_2) \cdot P(A|S_2)}{P(S_1) \cdot P(A|S_1)+P(S_2) \cdot P(A|S_2)+P(S_3) \cdot P(A|S_3)+P(S_4) \cdot P(A|S_4)}}\\ \\ P(S_2|\overline{A})=\displaystyle{\frac{P(S_2) \cdot P(\overline{A}|S_2)}{P(S_1) \cdot P(\overline{A}|S_1)+P(S_2) \cdot P(\overline{A}|S_2)+P(S_3) \cdot P(\overline{A}|S_3)+P(S_4) \cdot P(\overline{A}|S_4)}}\\ \\ P(S_3|A)=\displaystyle{\frac{P(S_3) \cdot P(A|S_3)}{P(S_1) \cdot P(A|S_1)+P(S_2) \cdot P(A|S_2)+P(S_3) \cdot P(A|S_3)+P(S_4) \cdot P(A|S_4)}}\\ \\ P(S_3|\overline{A})=\displaystyle{\frac{P(S_3) \cdot P(\overline{A}|S_3)}{P(S_1) \cdot P(\overline{A}|S_1)+P(S_2) \cdot P(\overline{A}|S_2)+P(S_3) \cdot P(\overline{A}|S_3)+P(S_4) \cdot P(\overline{A}|S_4)}}\\ \\ P(S_4|A)=\displaystyle{\frac{P(S_4) \cdot P(A|S_4)}{P(S_1) \cdot P(A|S_1)+P(S_2) \cdot P(A|S_2)+P(S_3) \cdot P(A|S_3)+P(S_4) \cdot P(A|S_4)}}\\ \\ P(S_4|\overline{A})=\displaystyle{\frac{P(S_4) \cdot P(\overline{A}|S_4)}{P(S_1) \cdot P(\overline{A}|S_1)+P(S_2) \cdot P(\overline{A}|S_2)+P(S_3) \cdot P(\overline{A}|S_3)+P(S_4) \cdot P(\overline{A}|S_4)}}\\ \\ \end{array}\right.$$

Diagramas de árbol

Ejemplos:

Tablas de contingencia

Ejemplo:

Resultados teóricos importantes

Diagramas de Venn

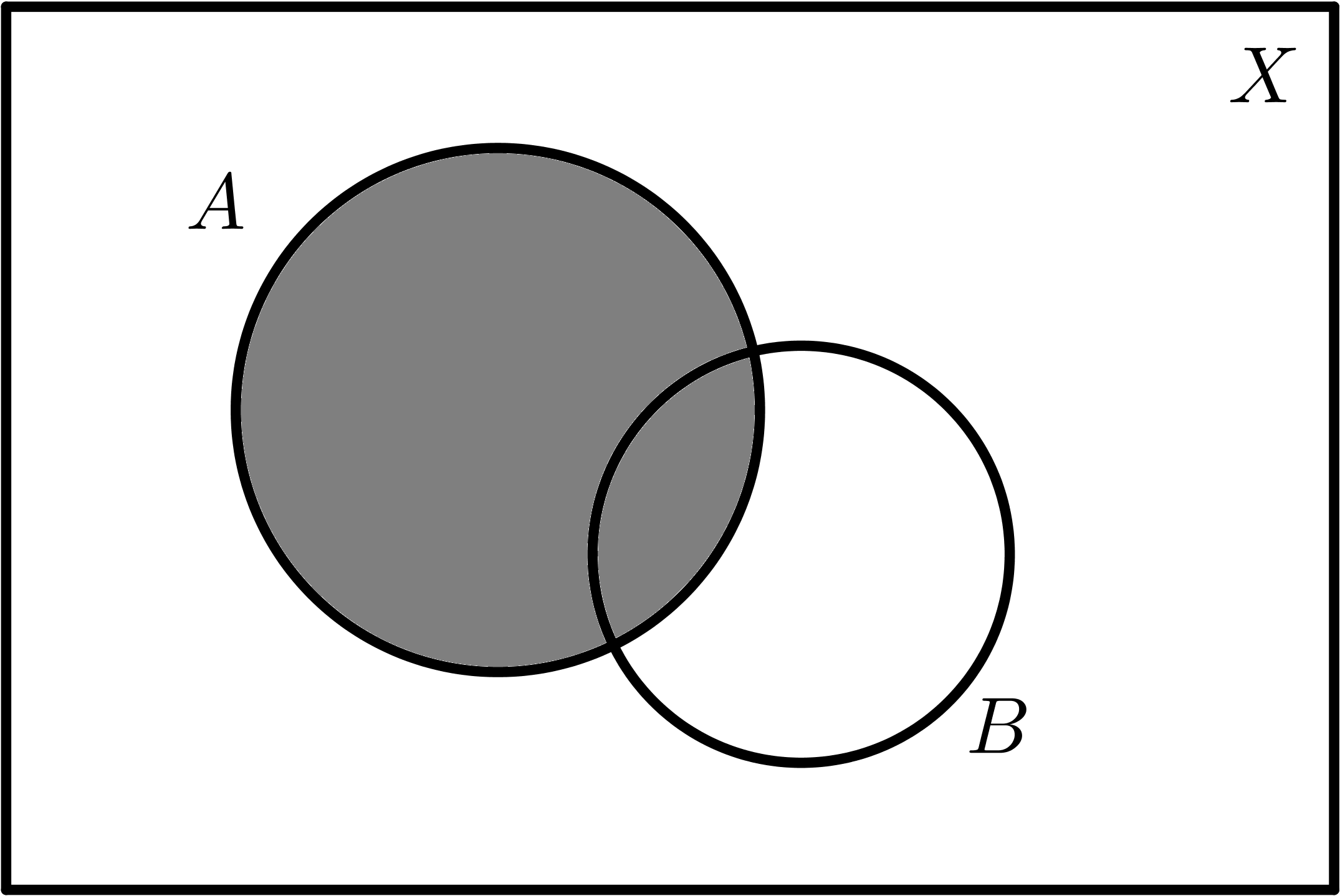
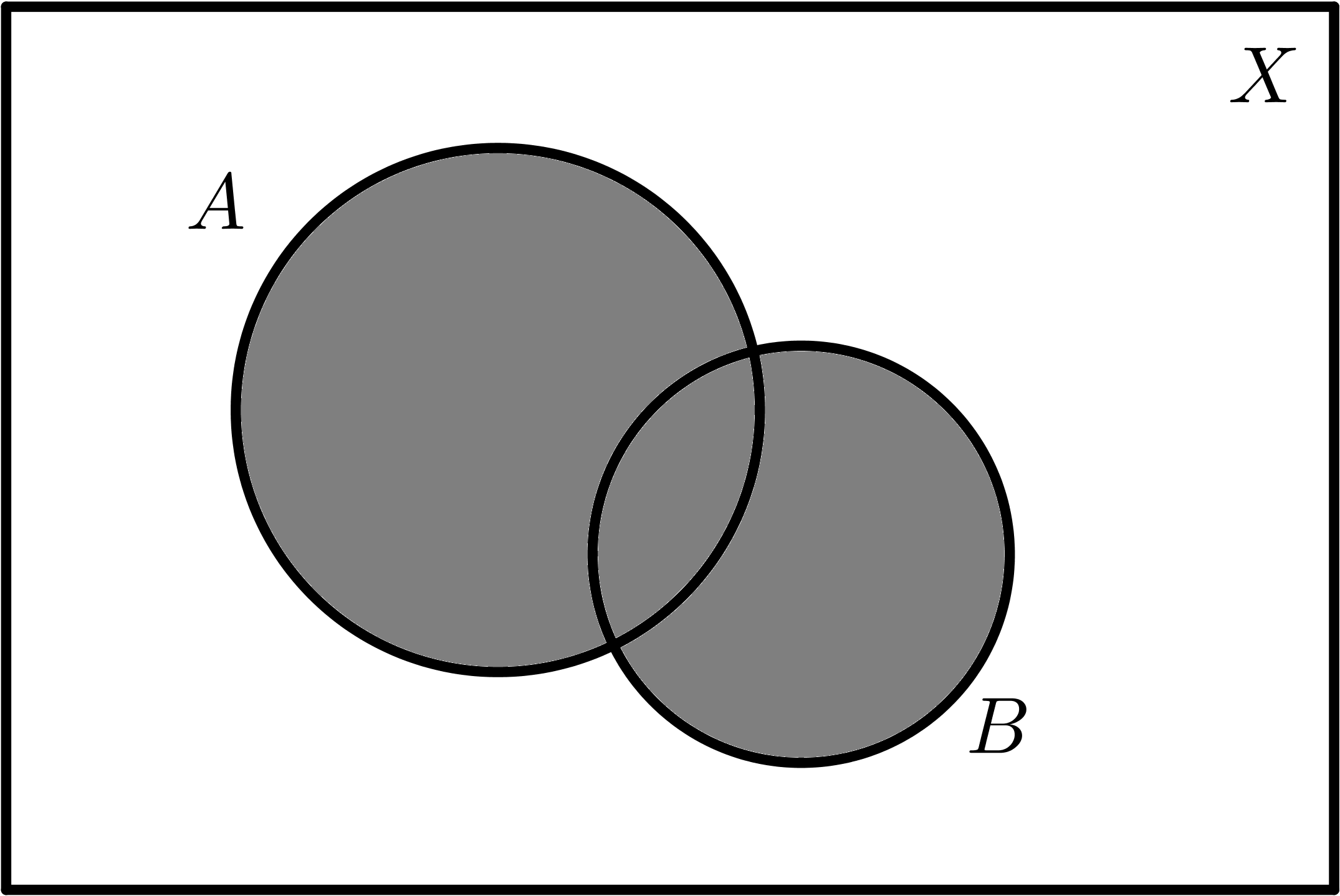
Dados dos conjuntos A y B:


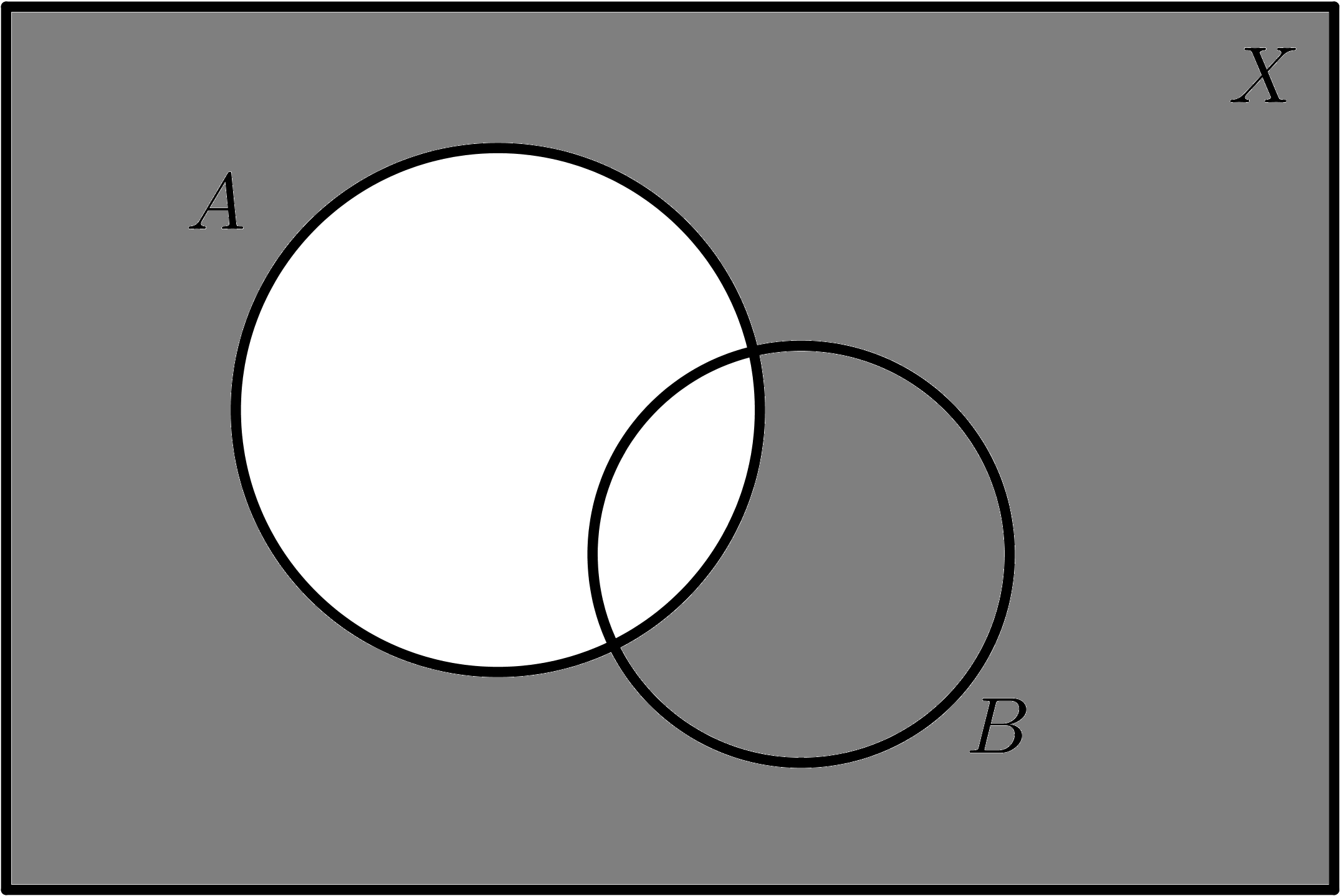
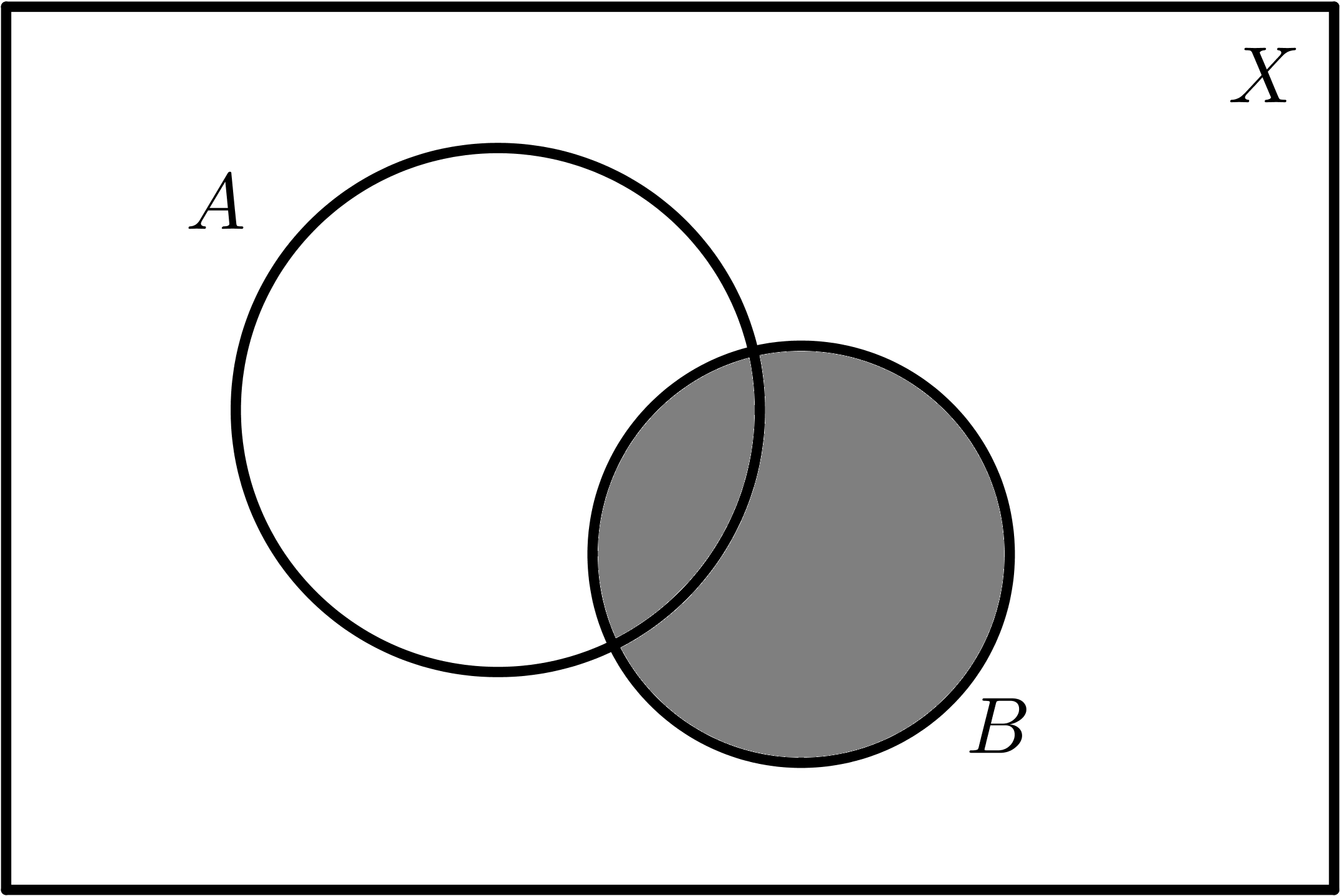
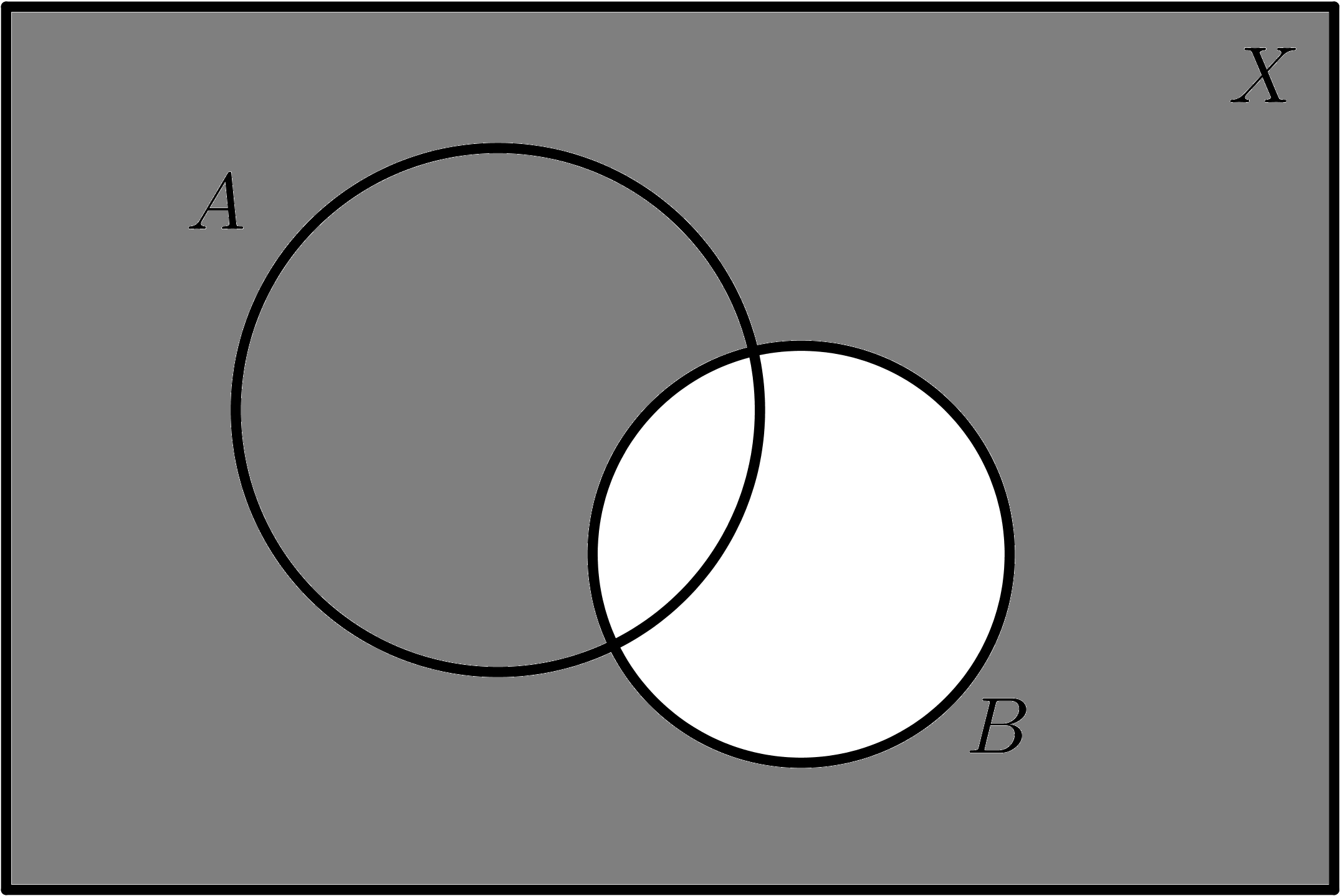
$$A$$	$$\overline{A}$$	$$B$$	$$\overline{B}$$

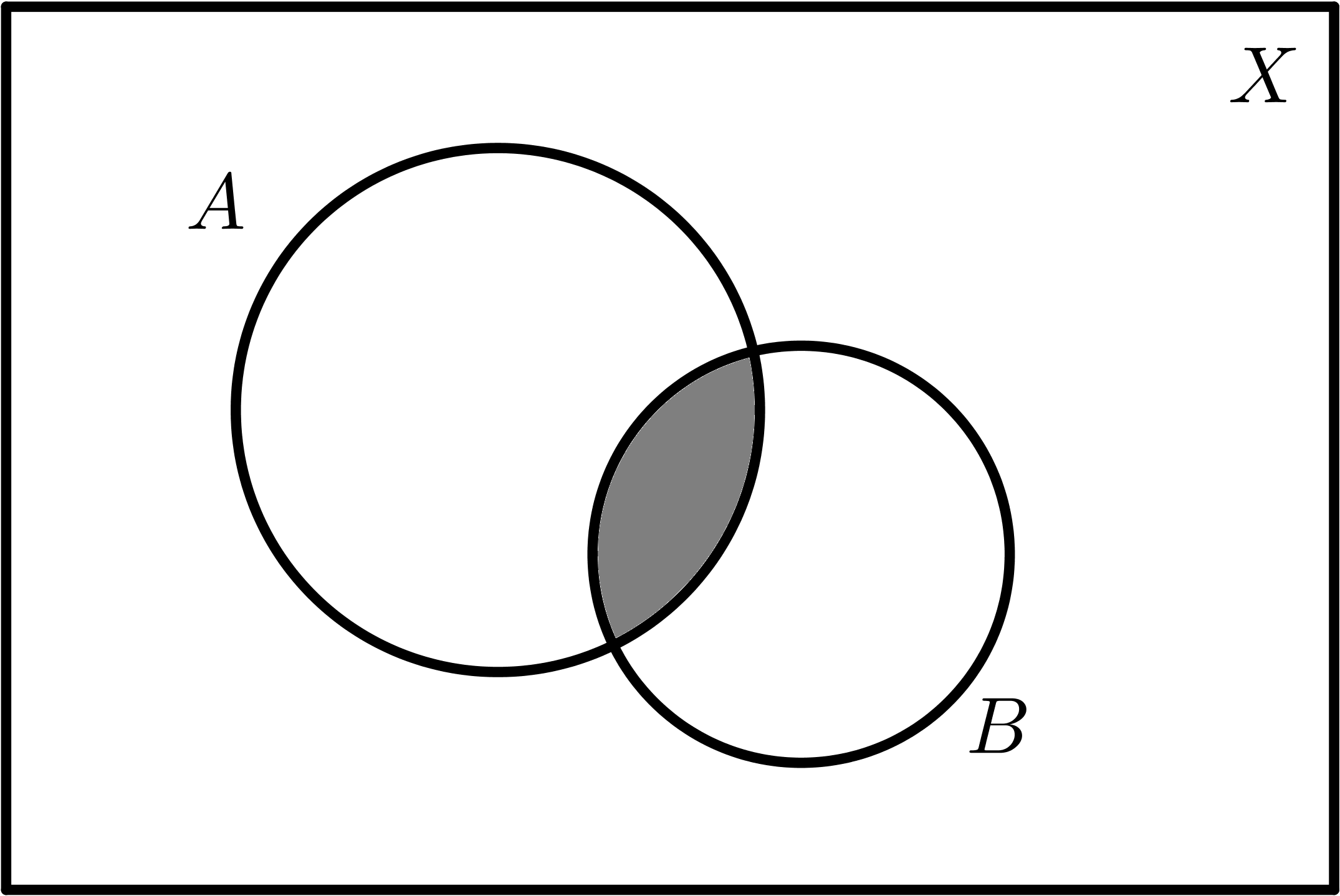
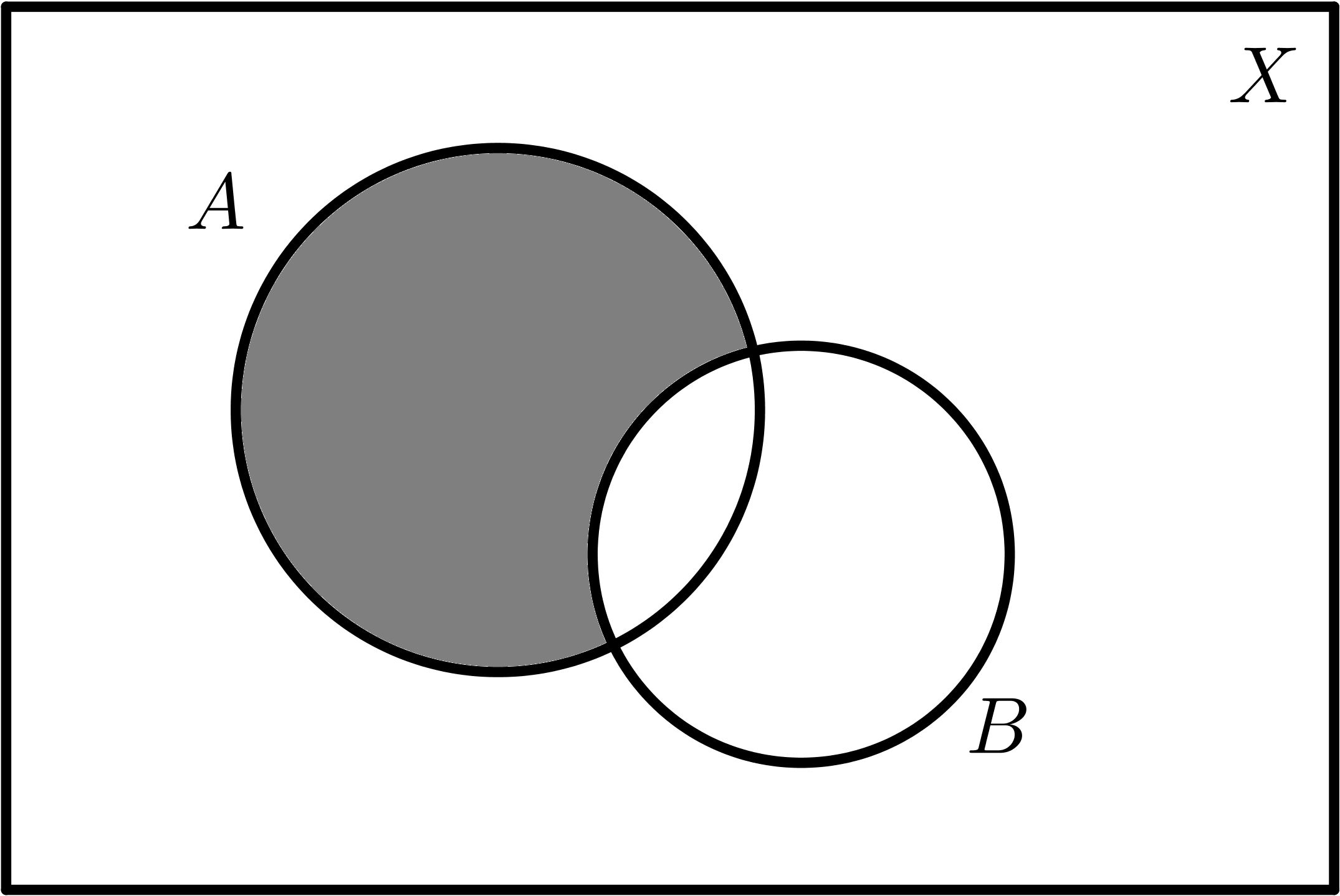
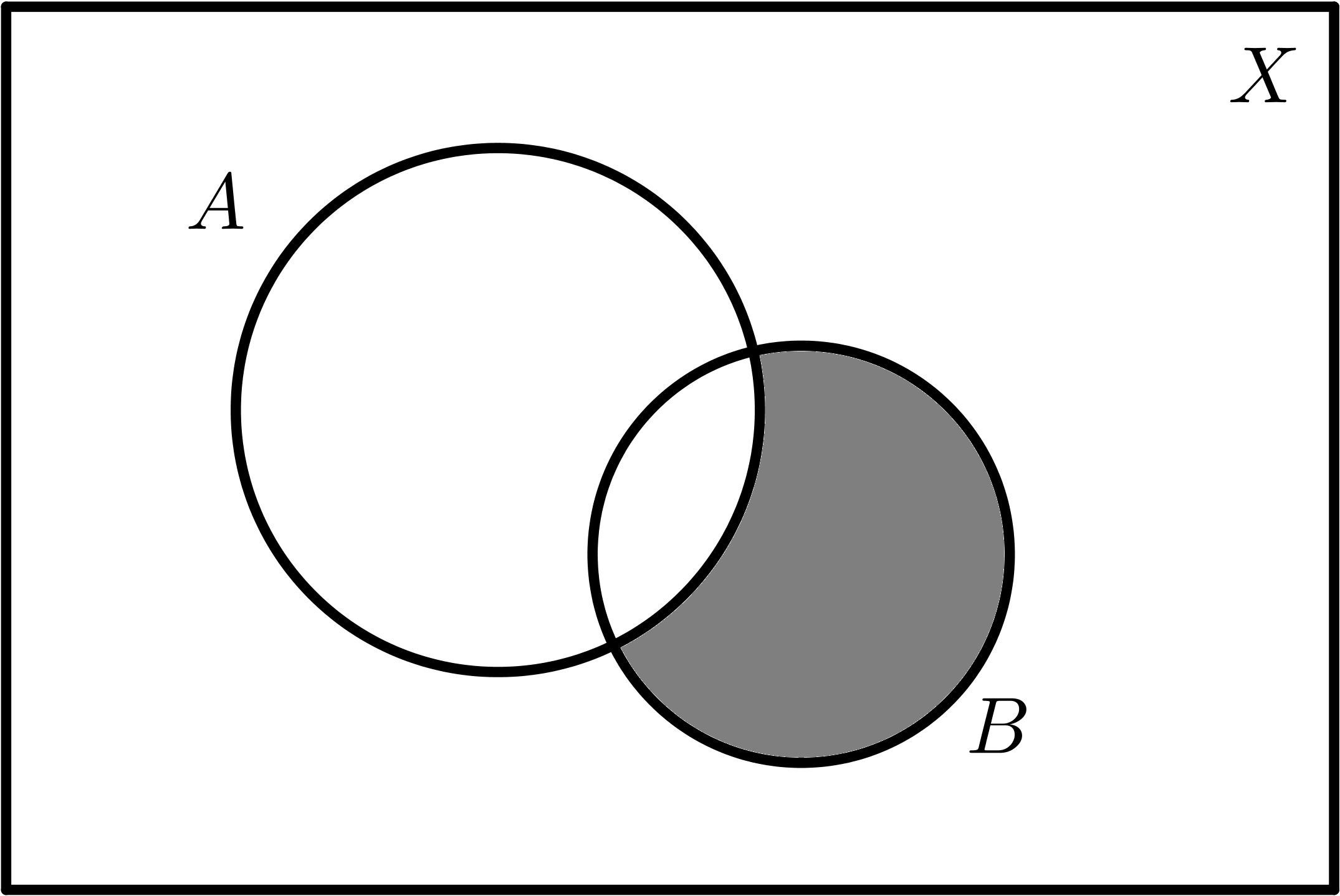
$$A \cup B$$	$$A \cap B$$	$$A - B$$	$$B - A$$

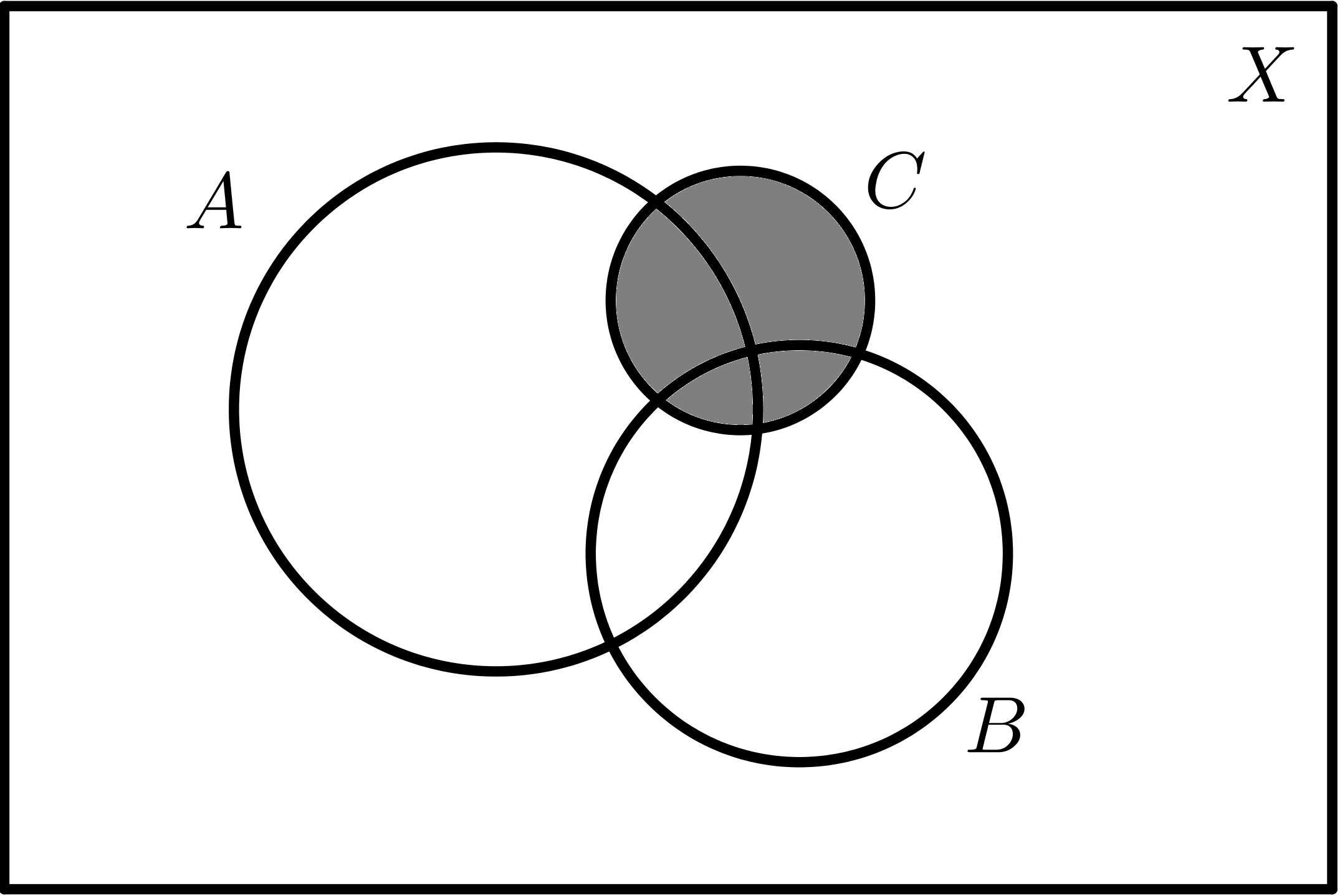
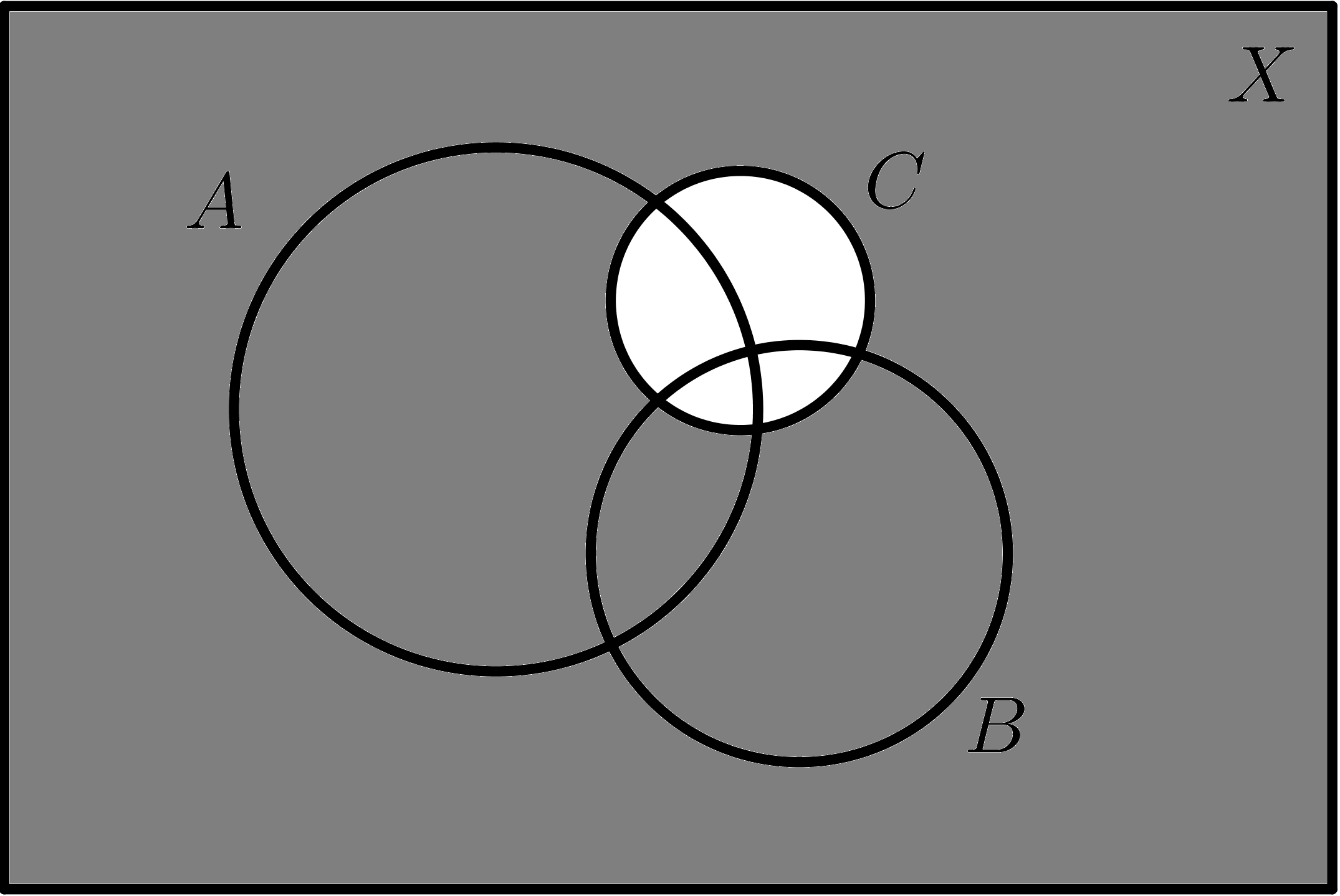
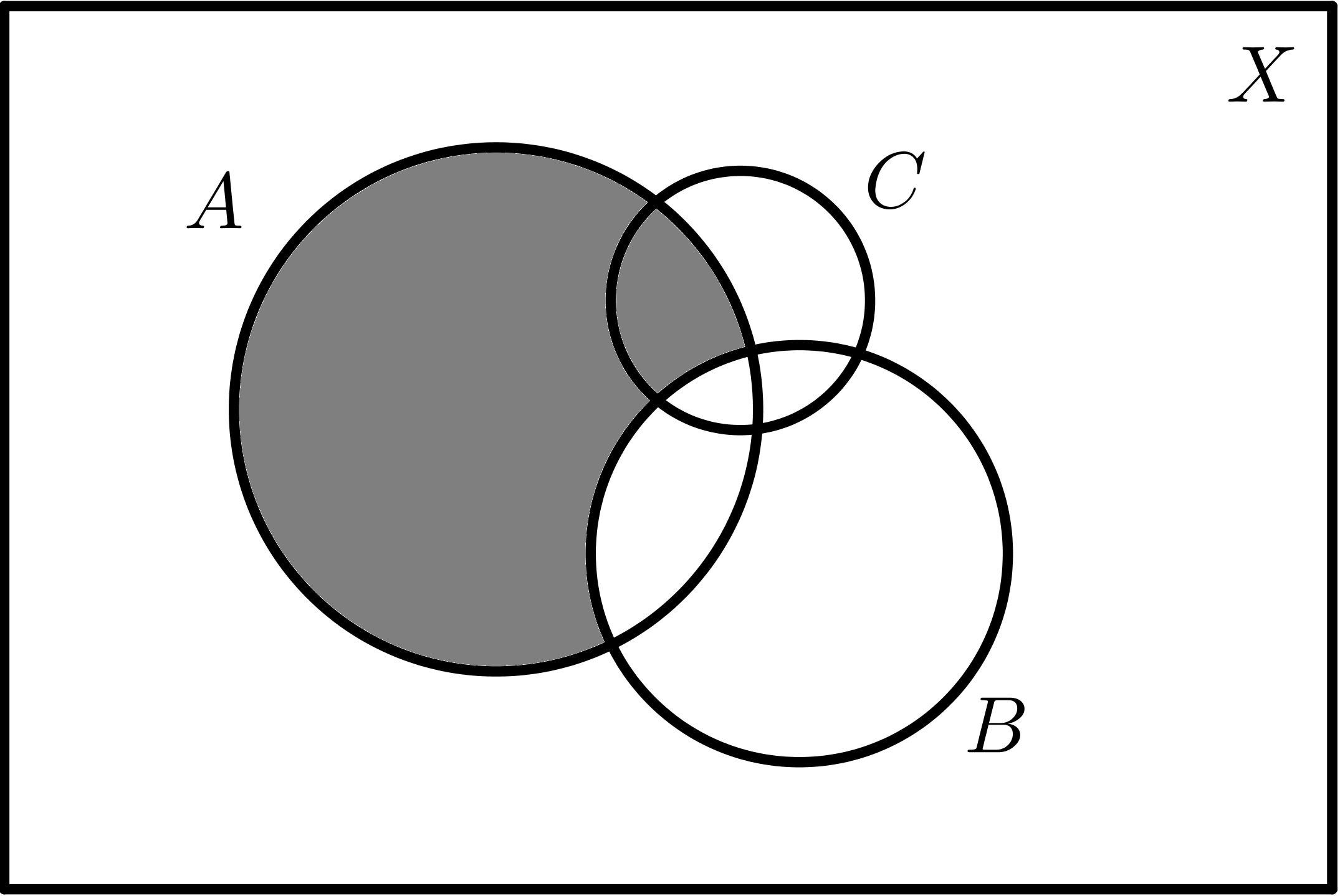
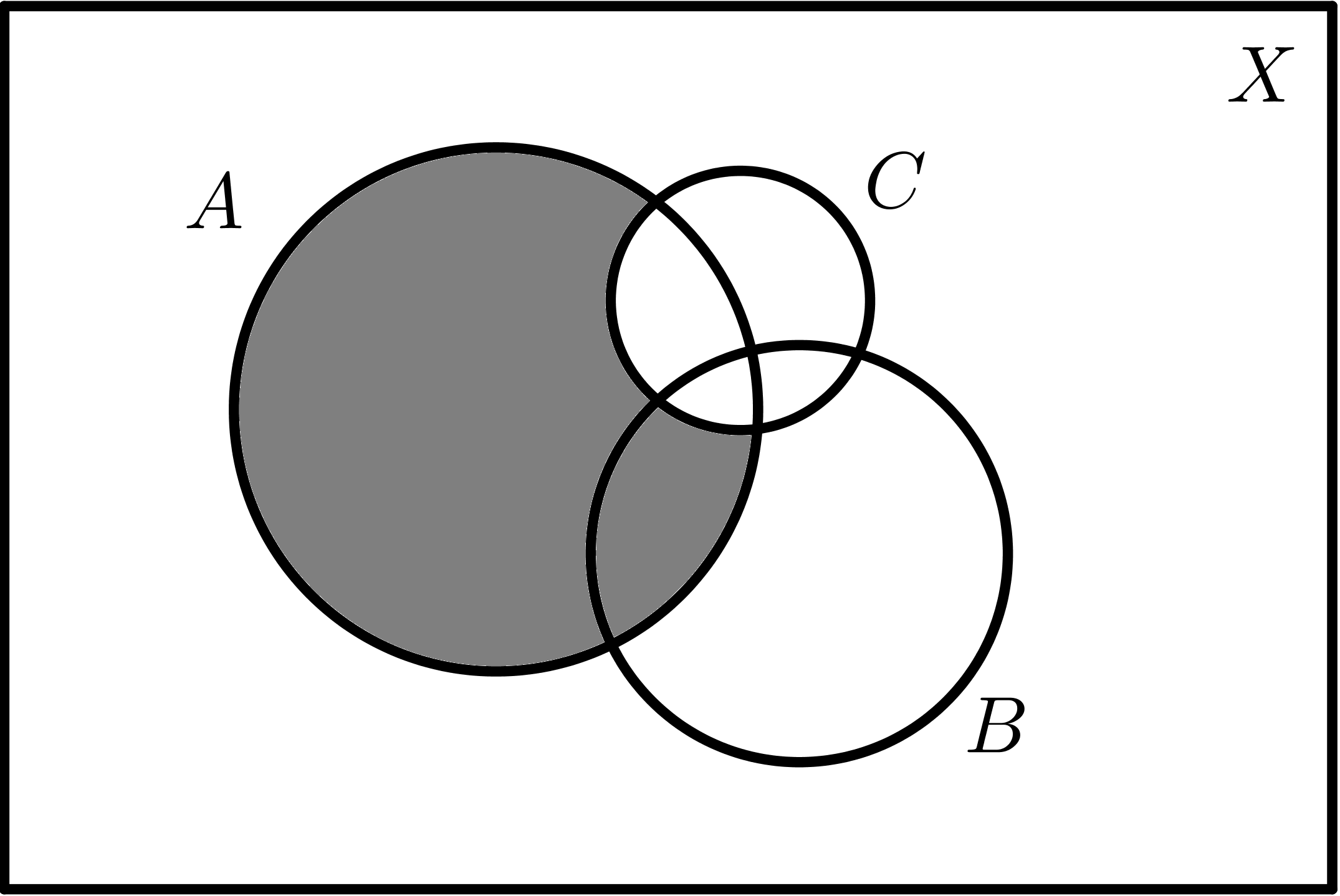
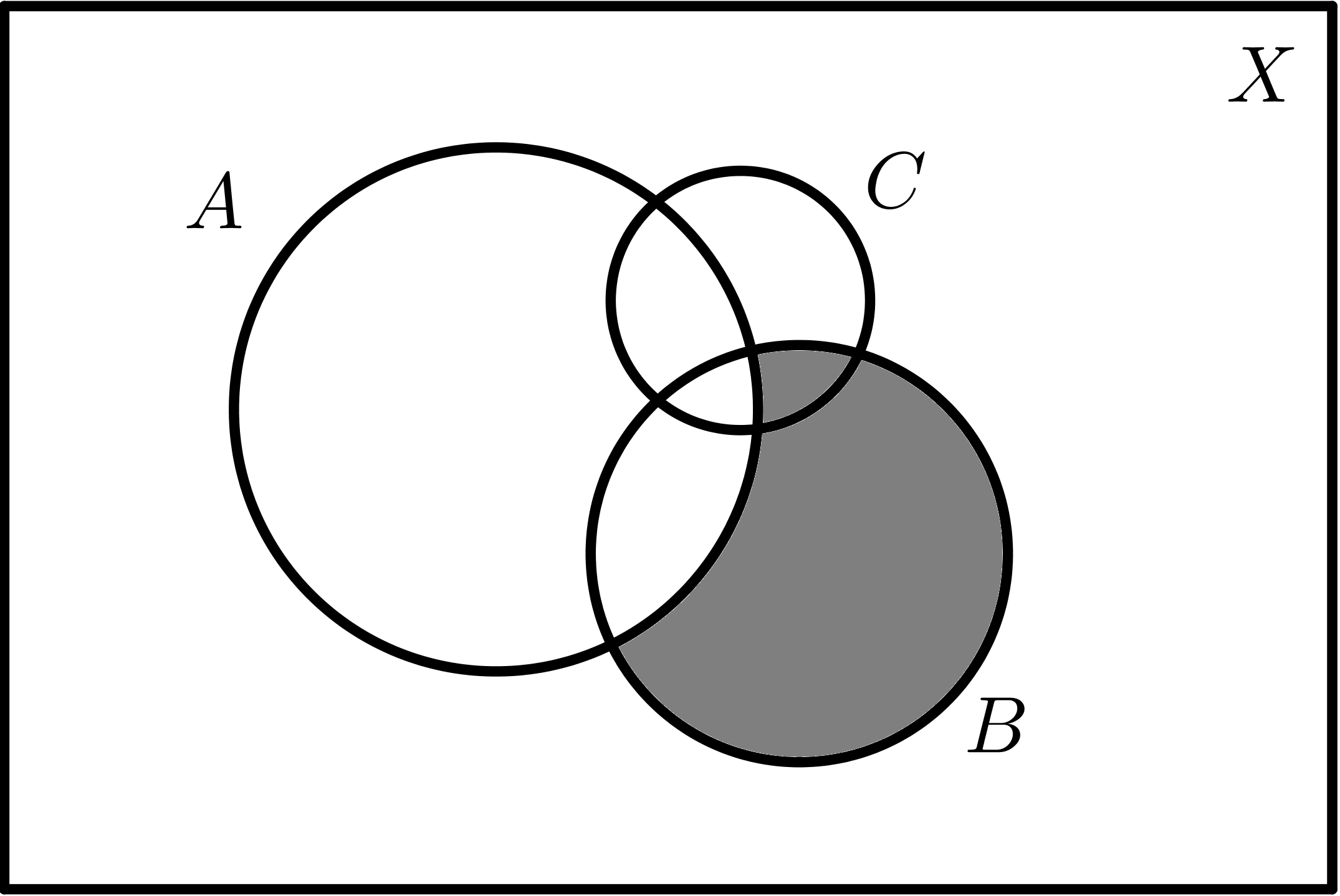
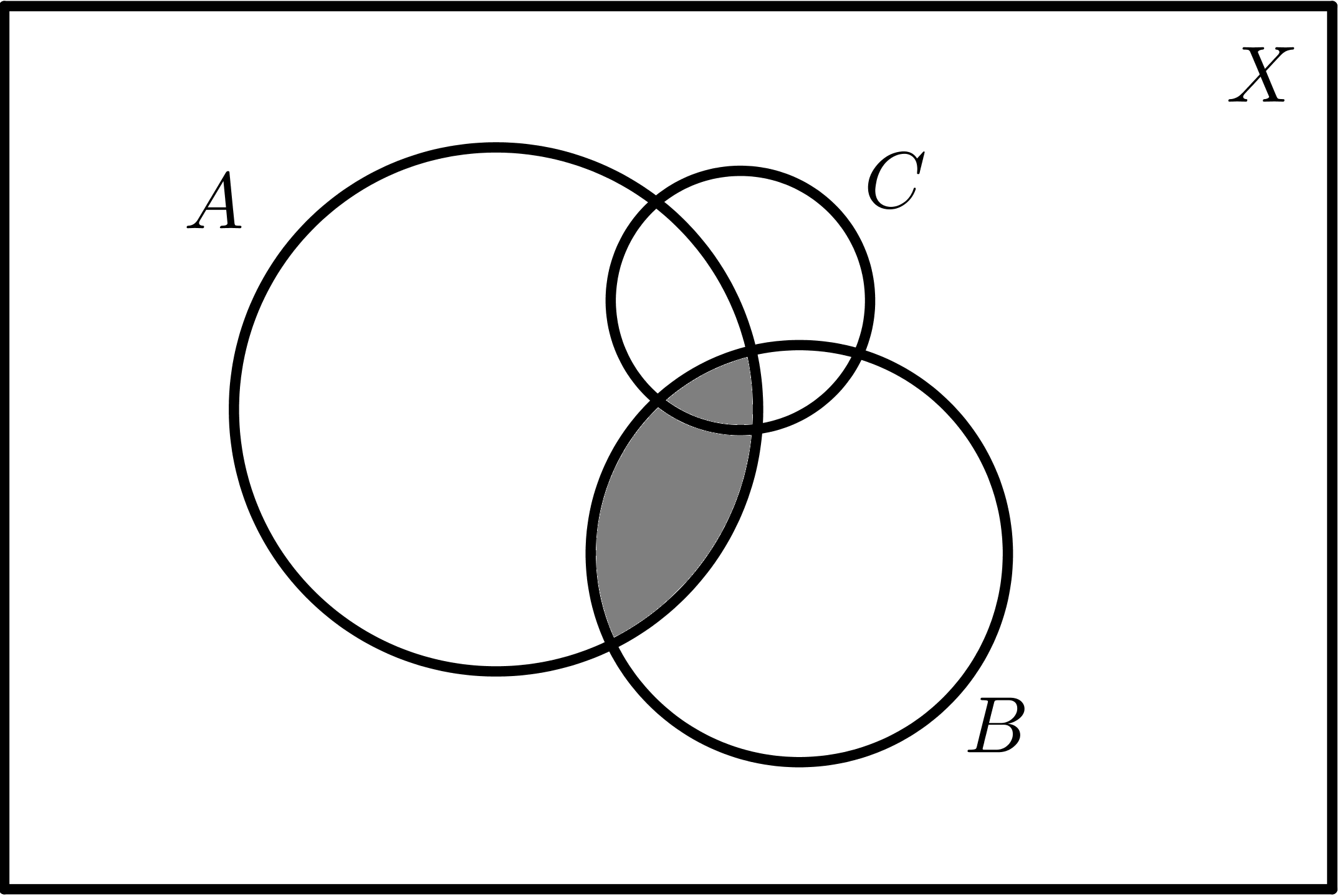
Dados tres conjuntos A, B y C:


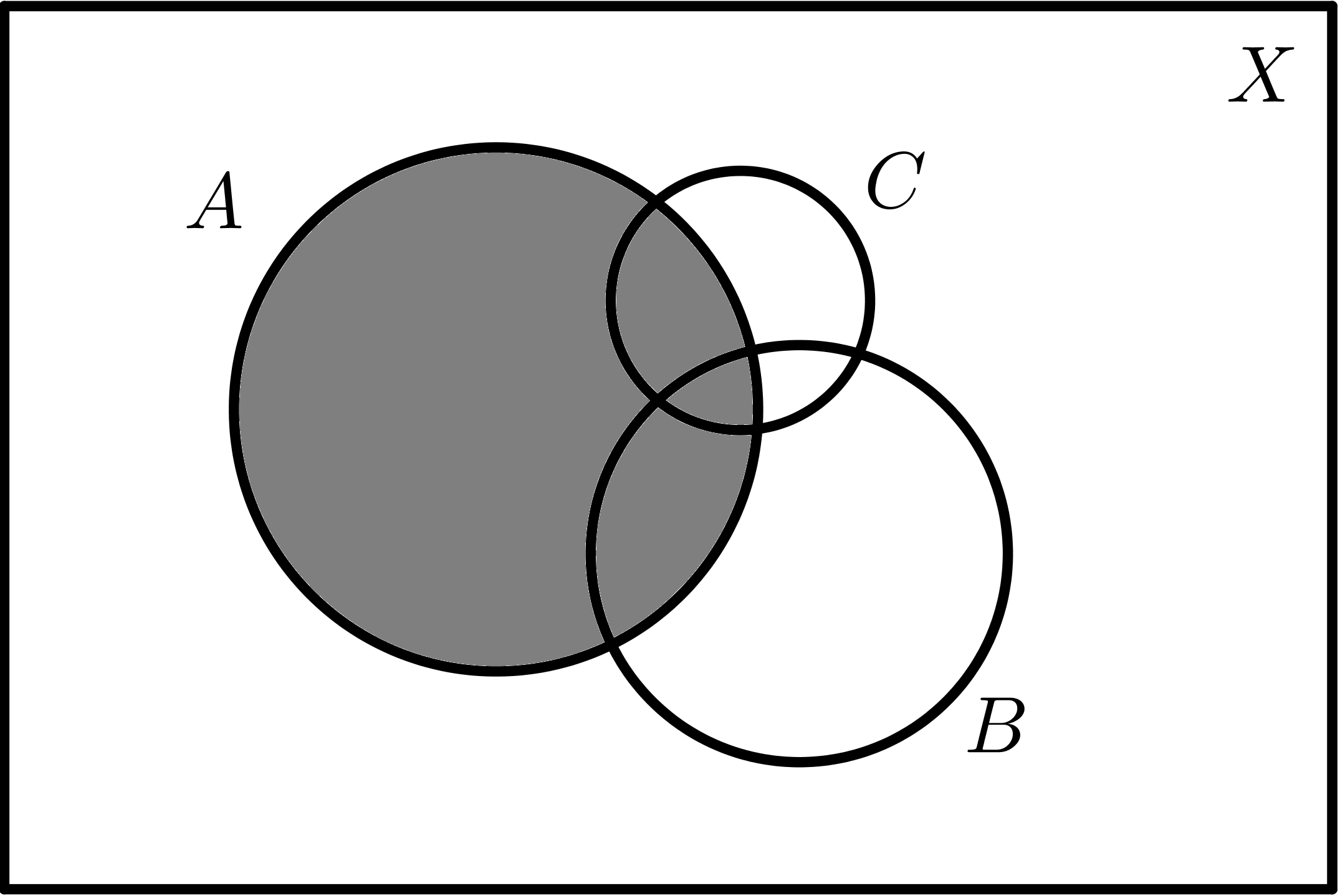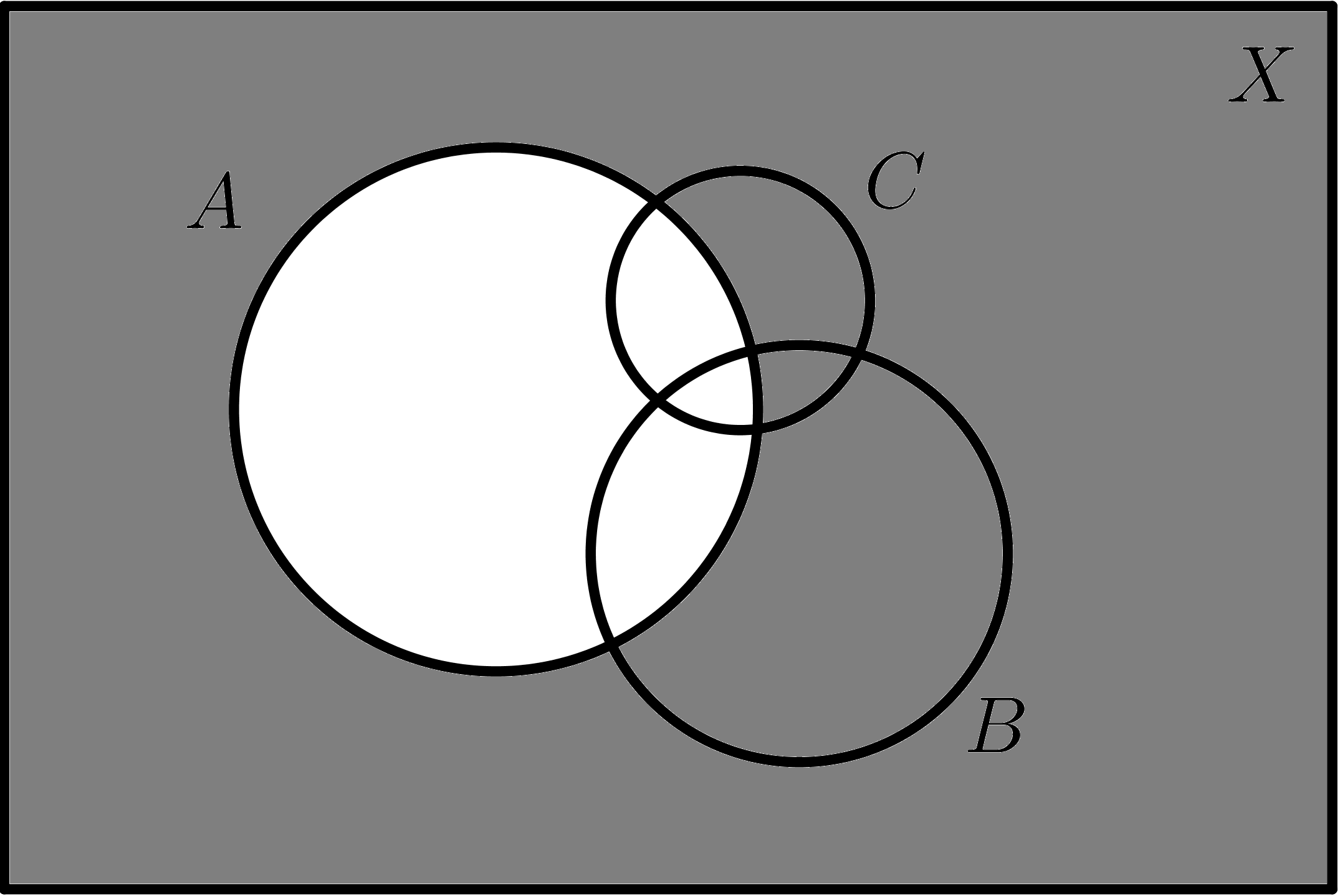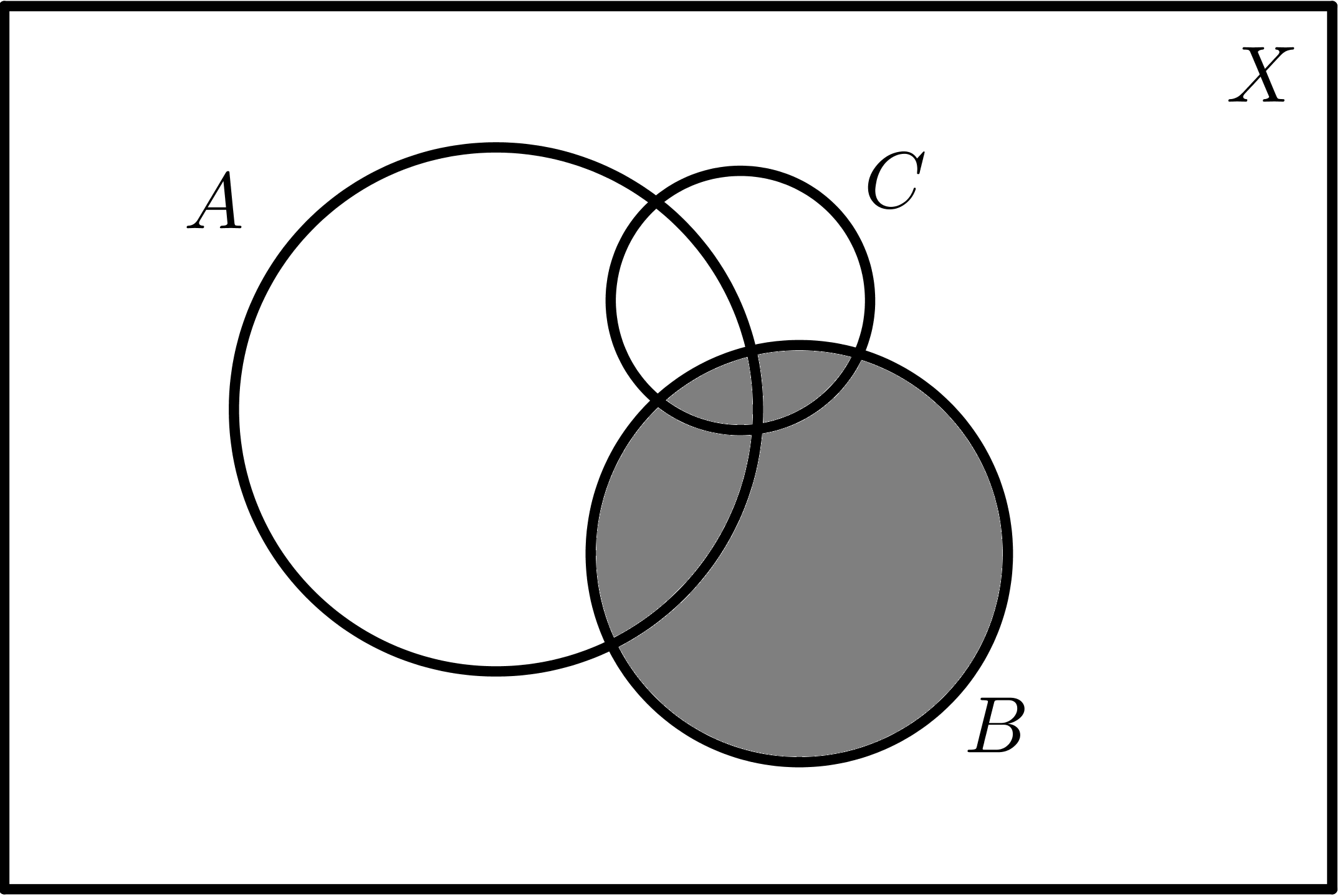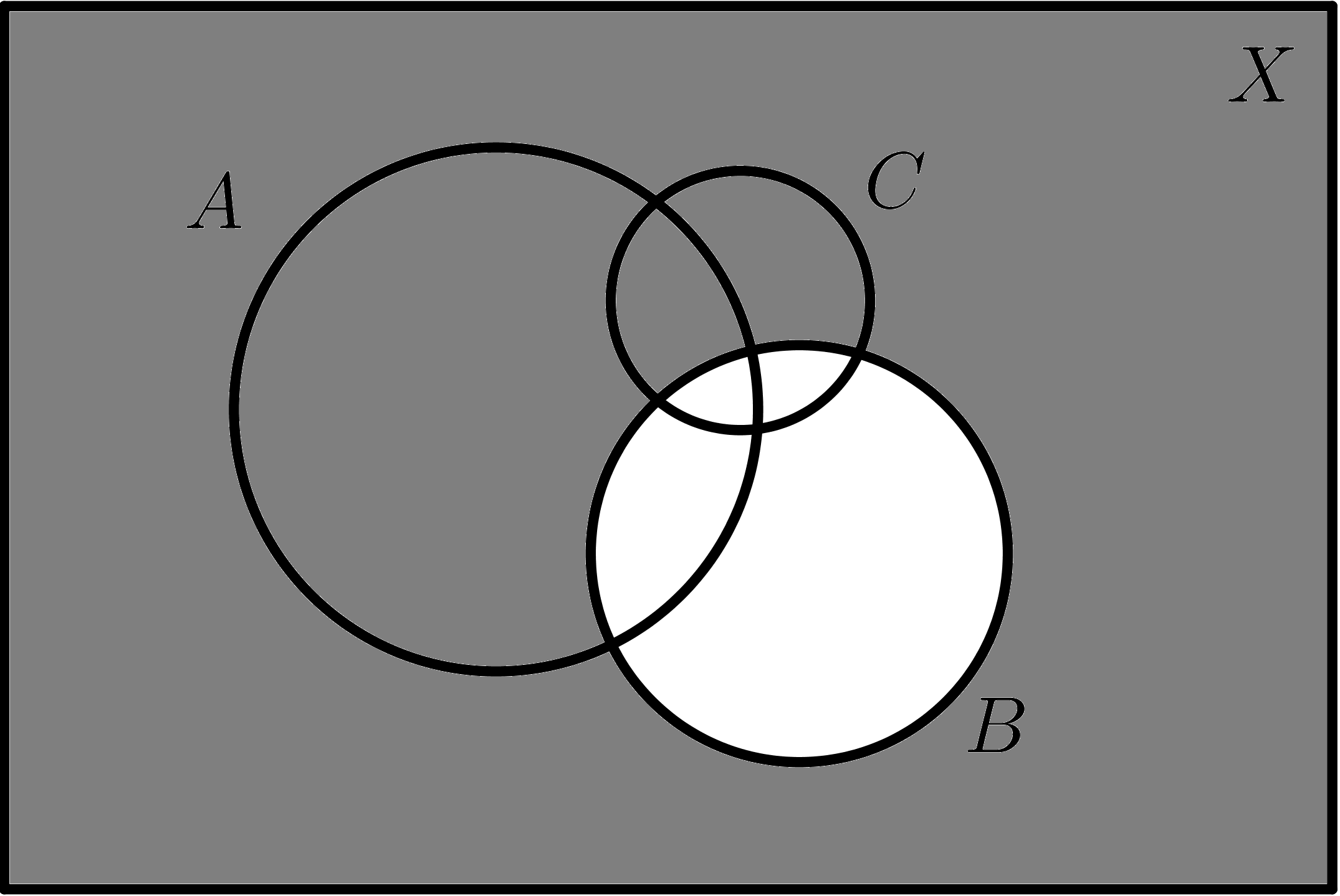$$A$$	$$\overline{A}$$	$$B$$	$$\overline{B}$$

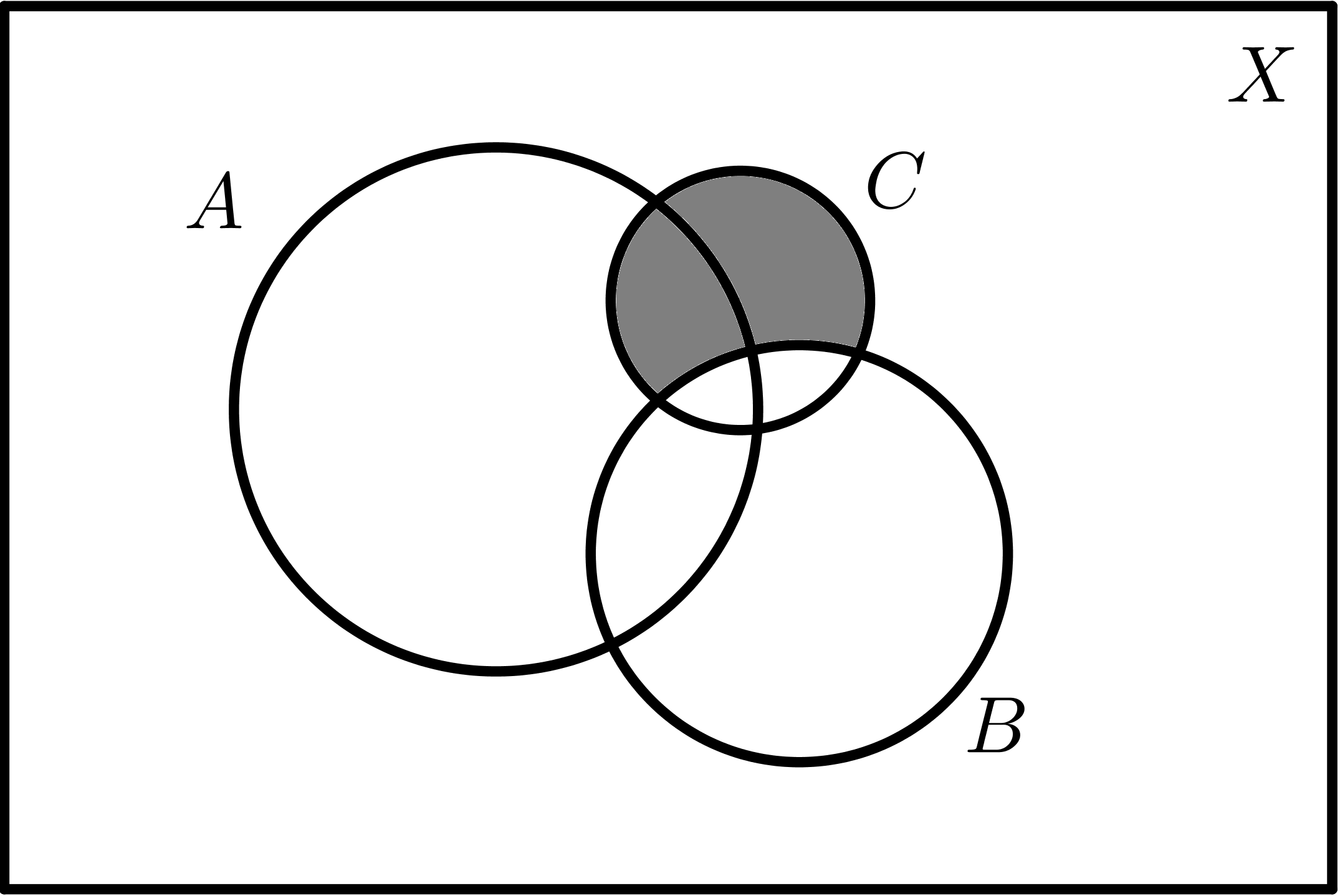
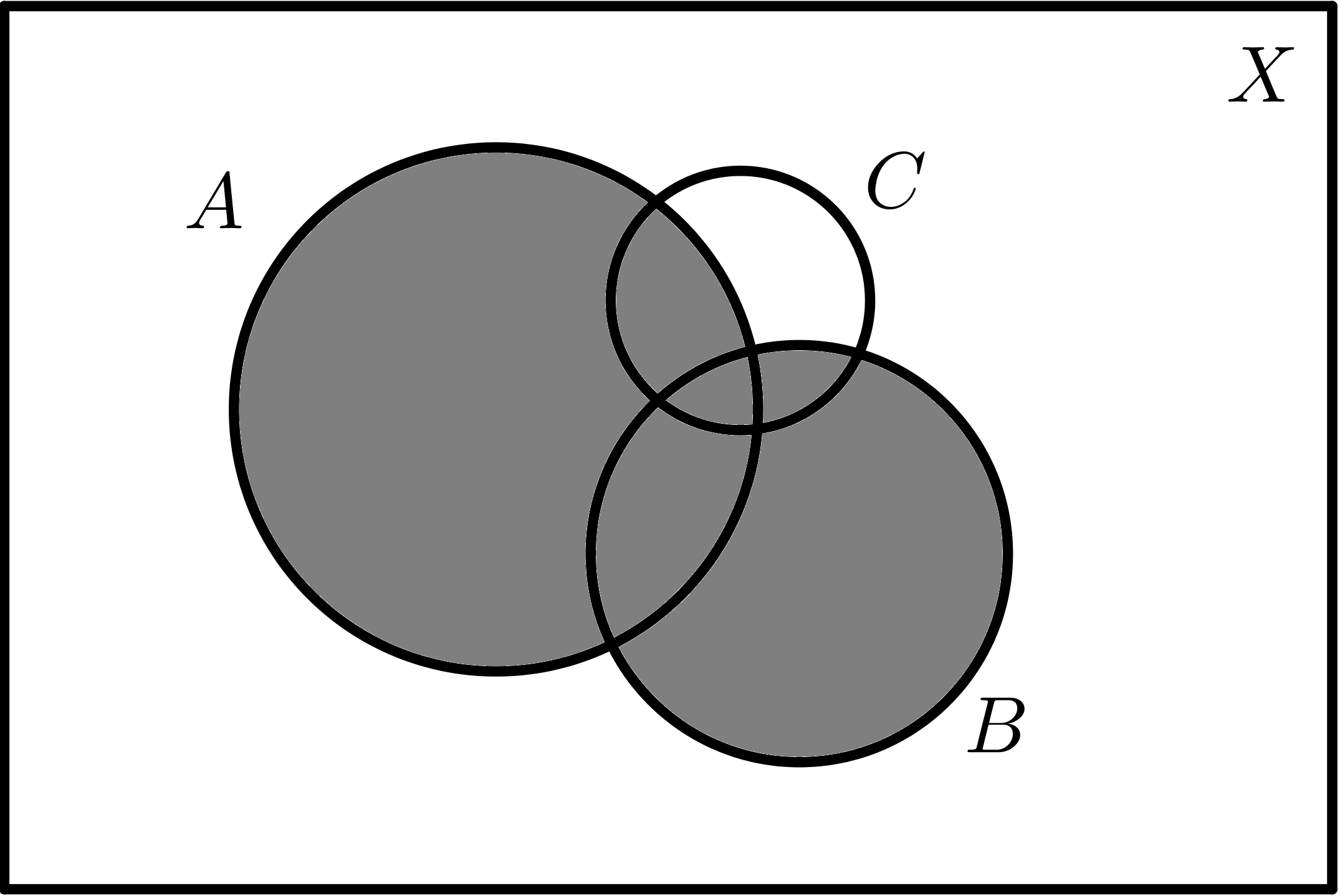
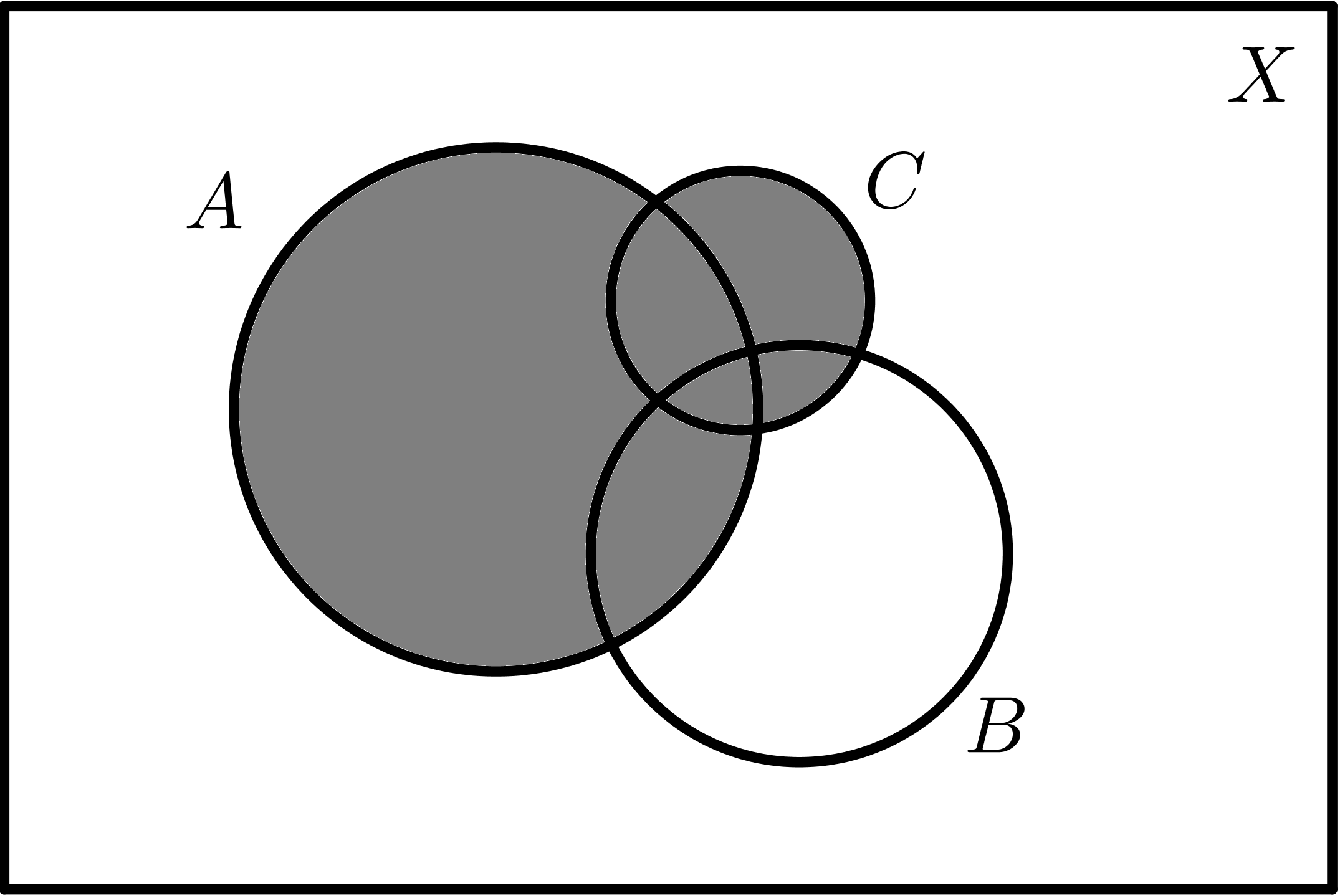
$$C$$	$$\overline{C}$$	$$A - B$$	$$A - C$$

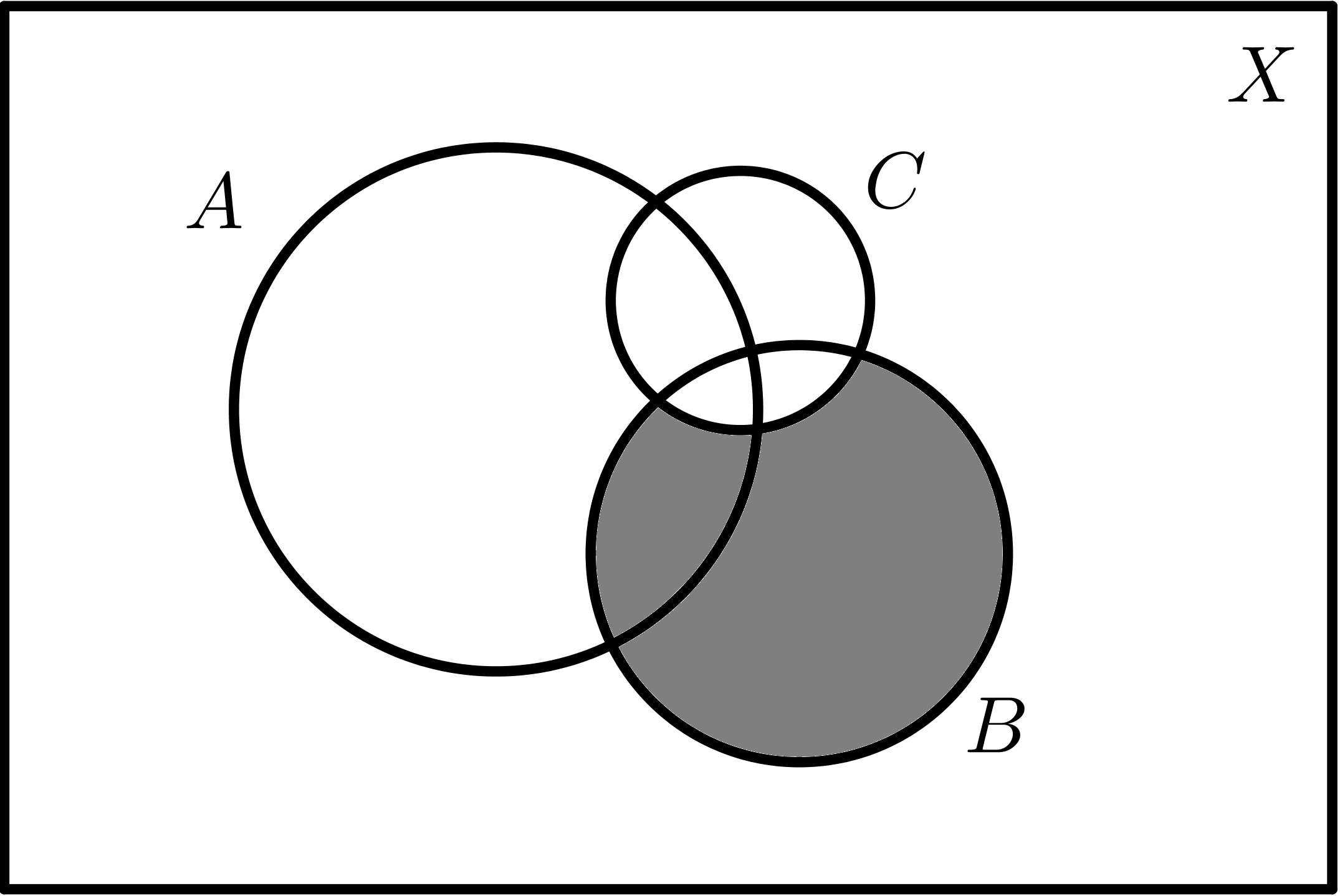
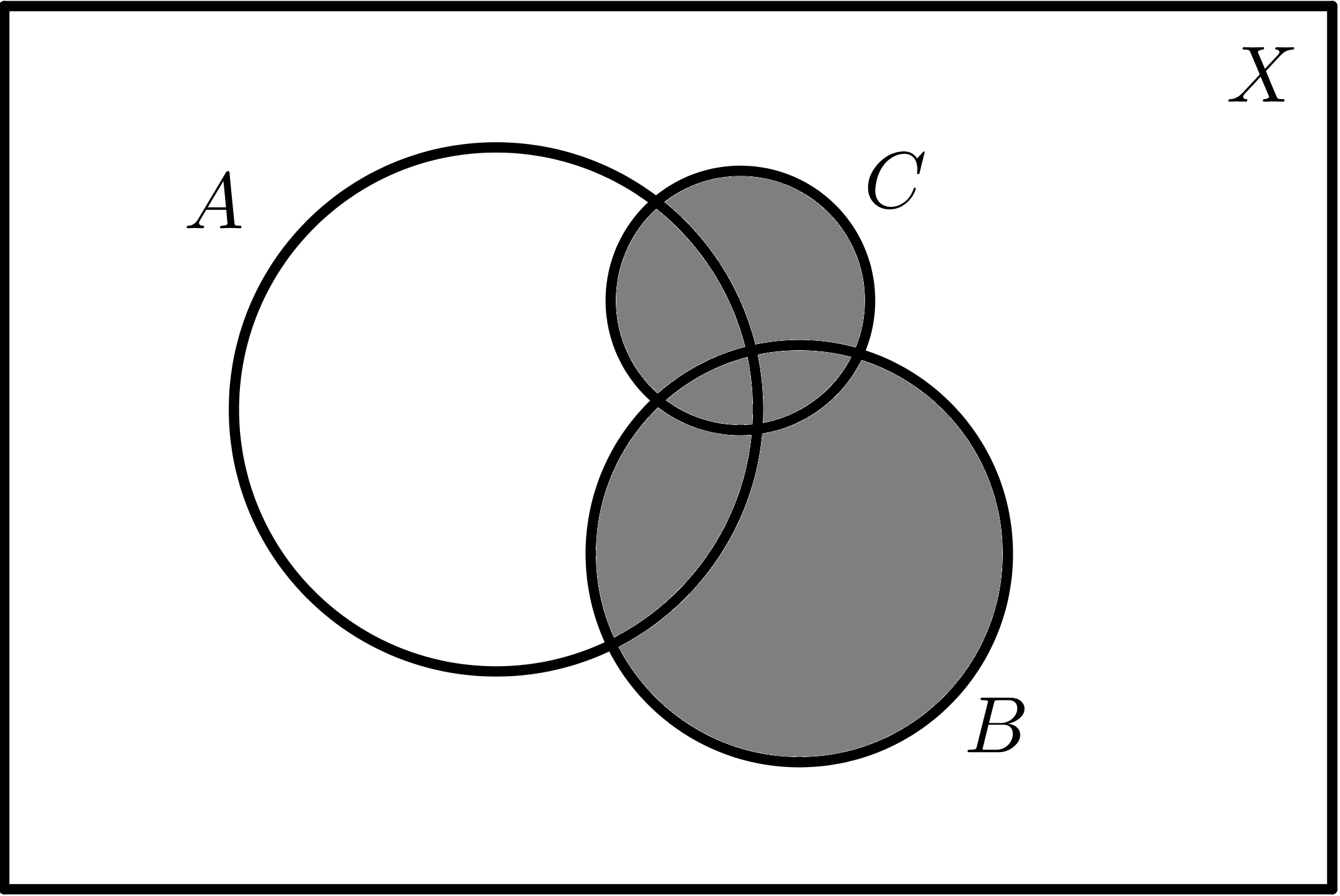
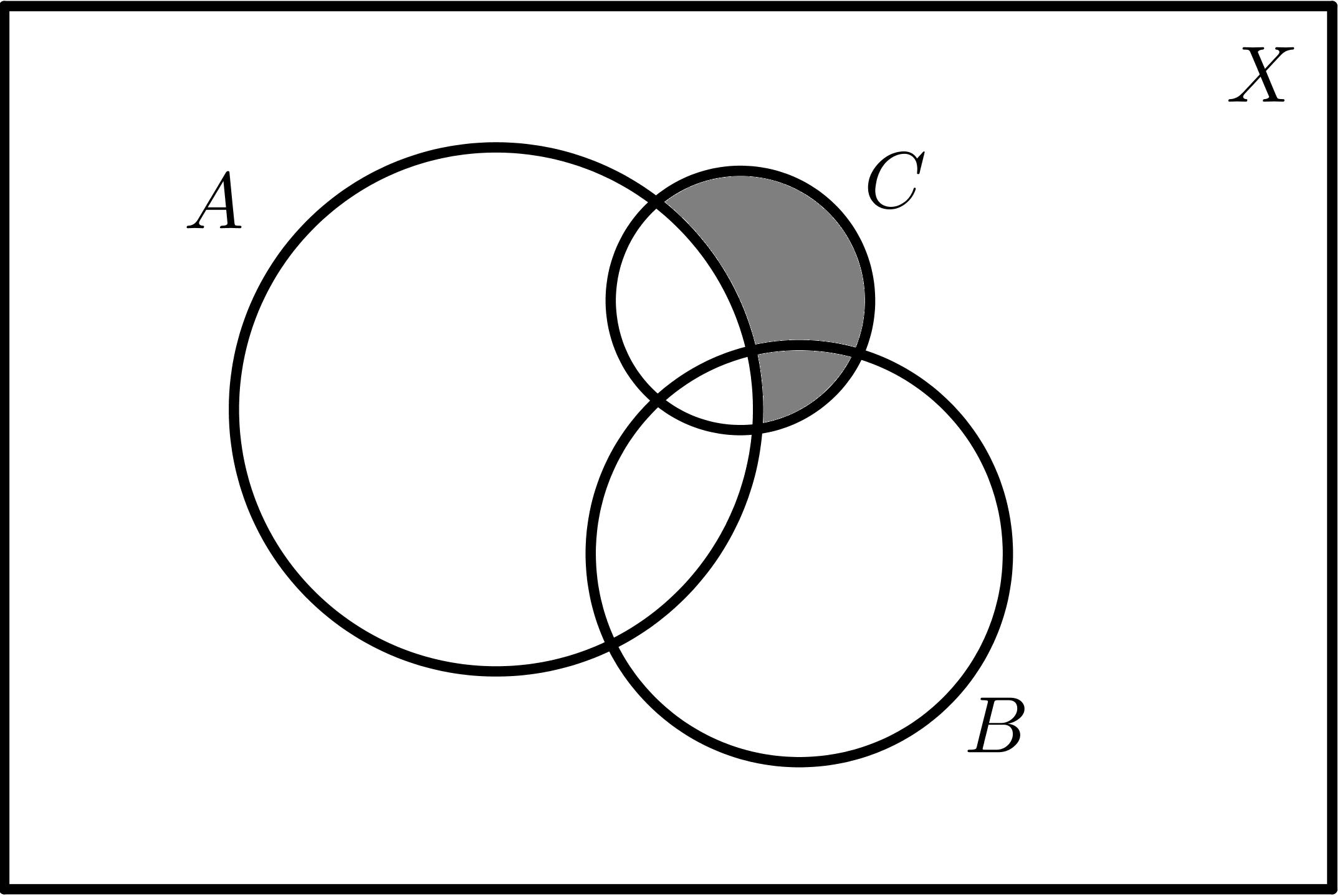
$$B - A$$	$$B - C$$	$$C - A$$	$$C - B$$

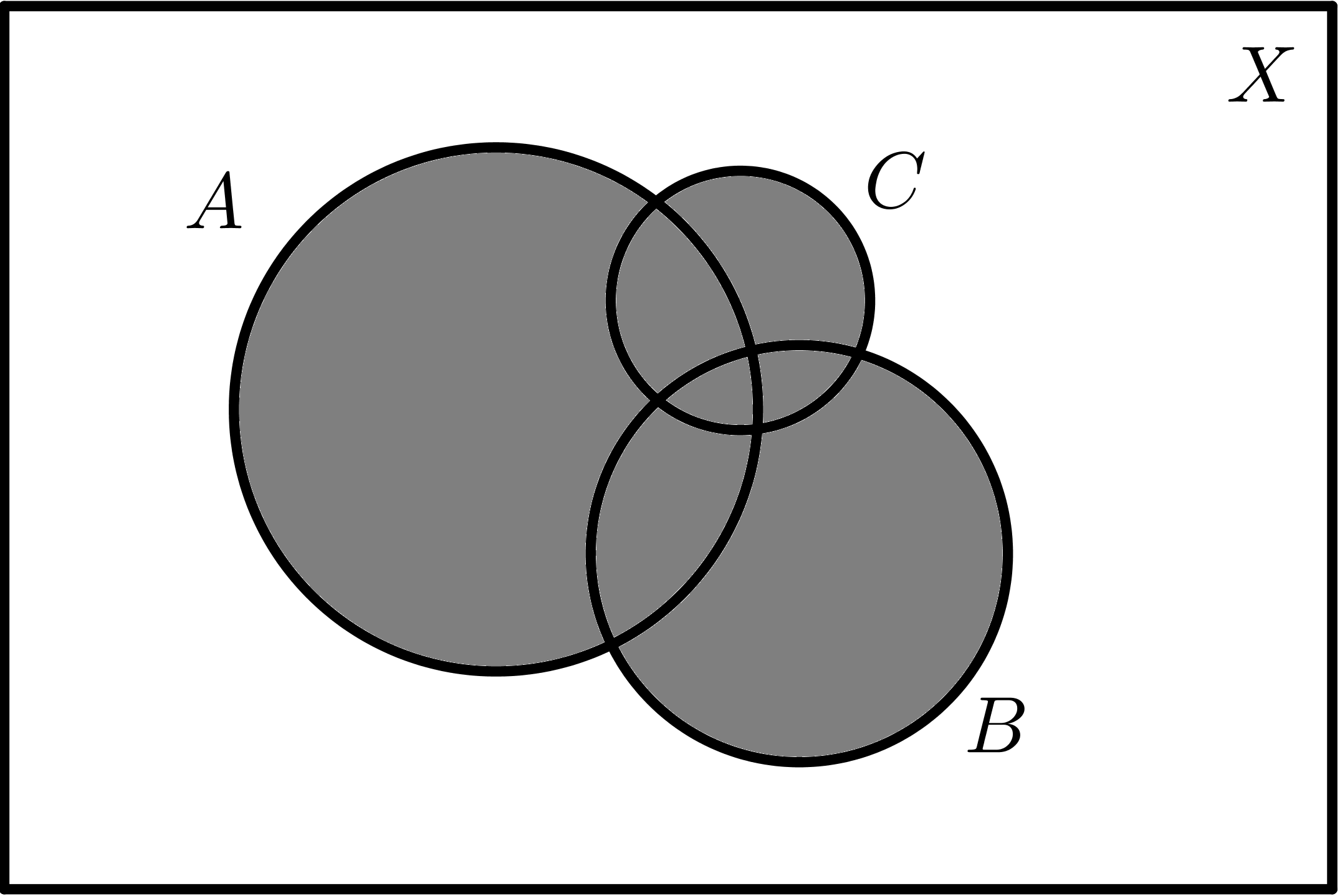$$A \cup B$$	$$A \cup C$$	$$B \cup C$$	$$A \cup B \cup C$$

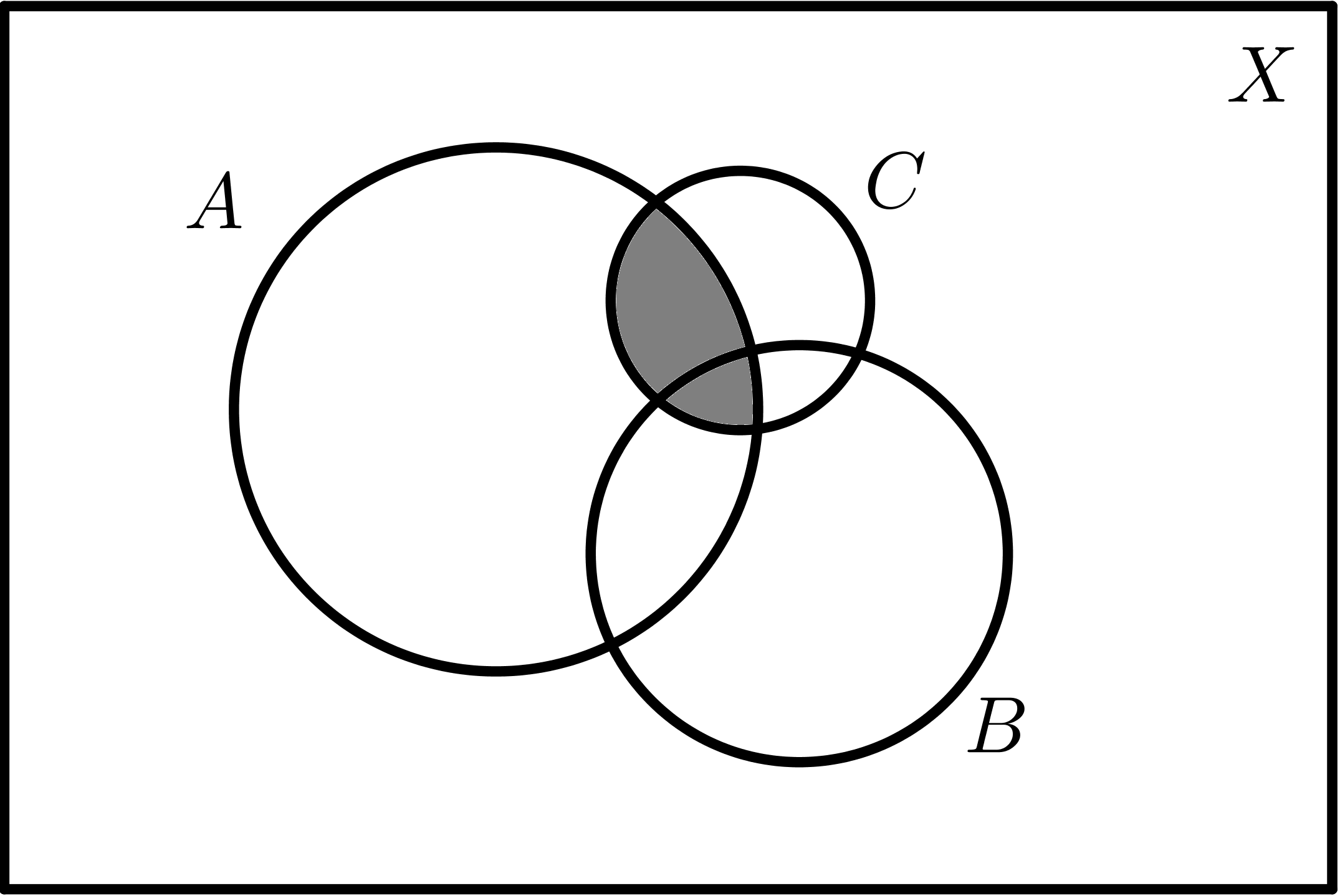
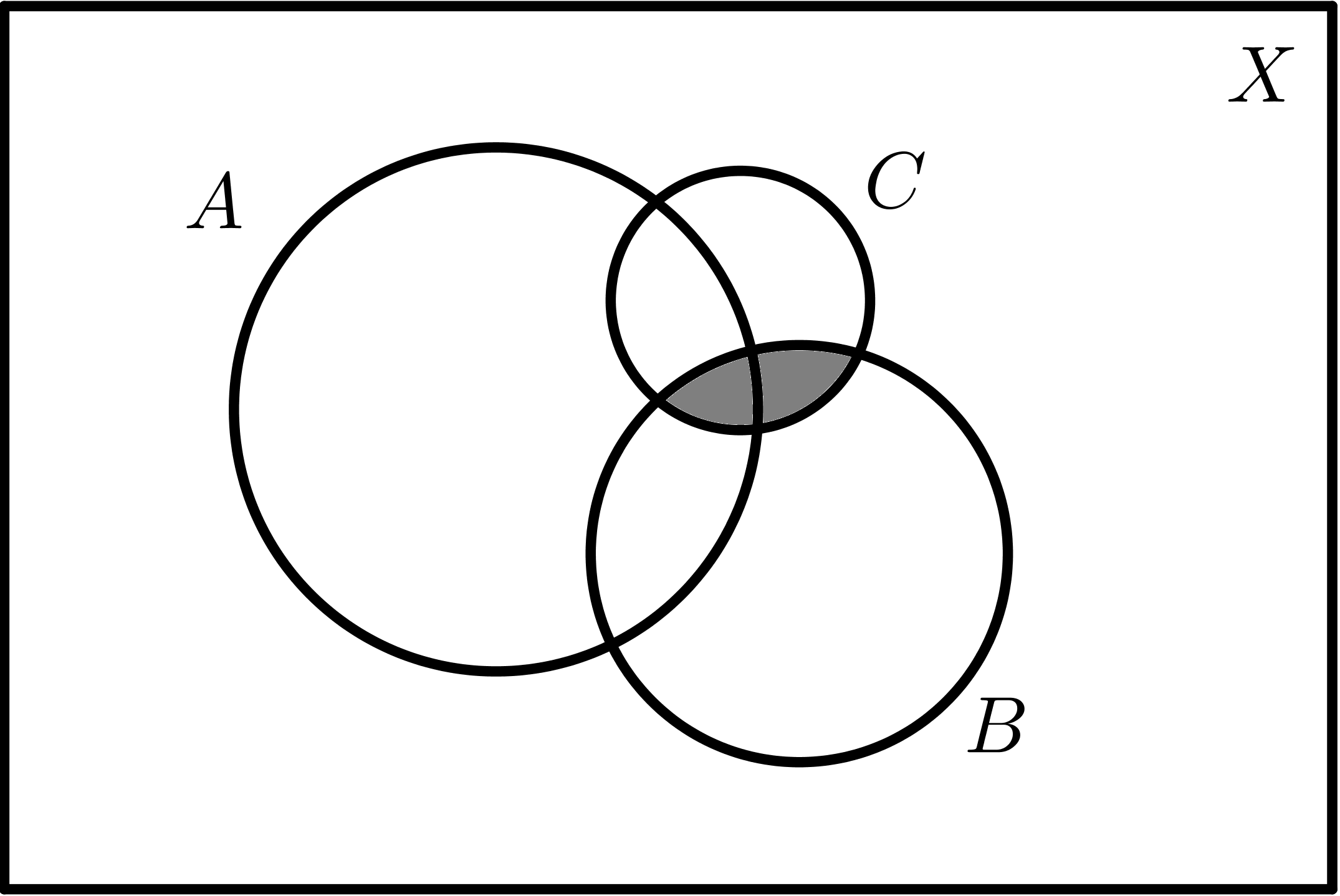
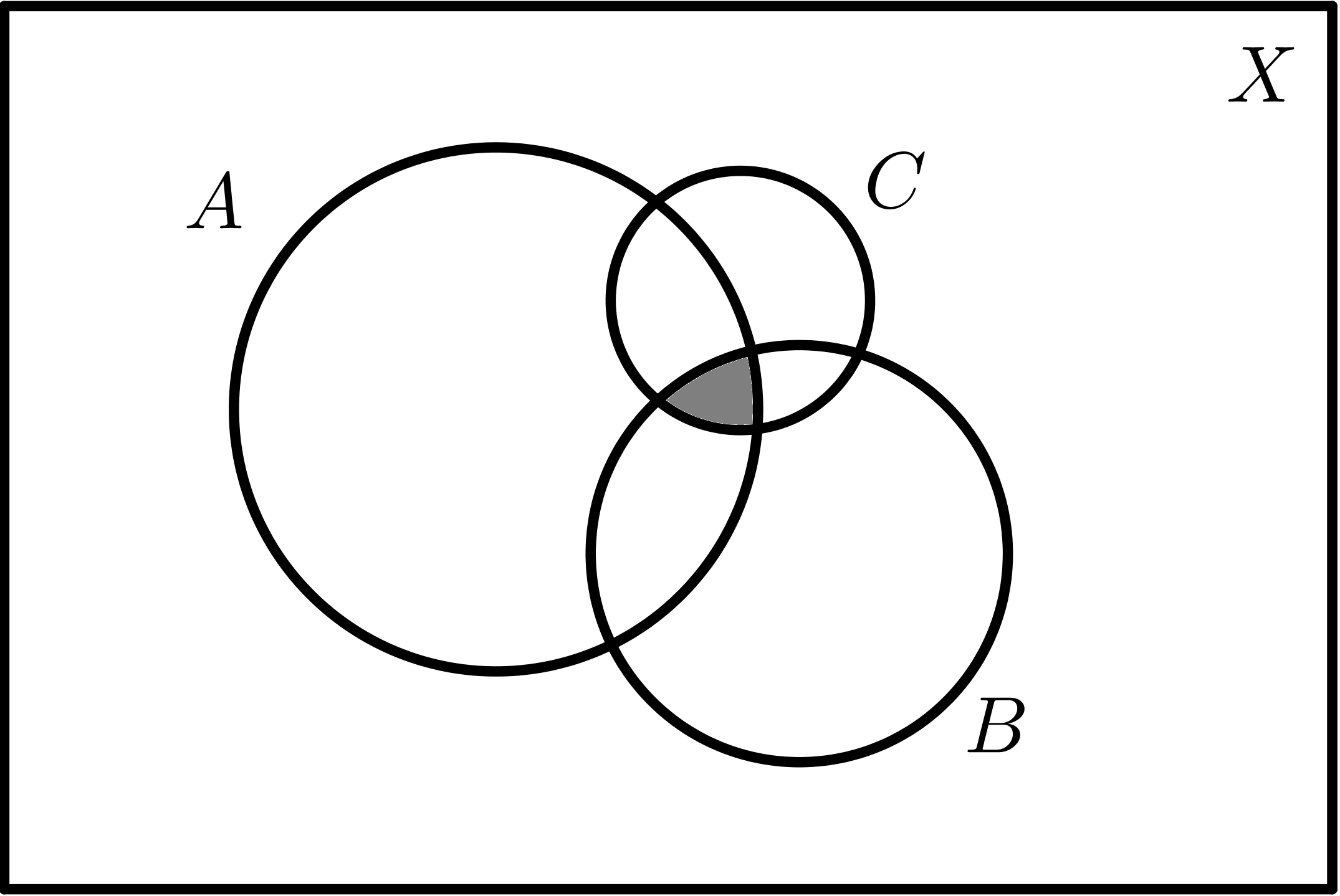
$$A \cap B$$	$$A \cap C$$	$$B \cap C$$	$$A \cap B \cap C$$

Combinatoria

Números Combinatorios

$$\left\{\begin{array}{l} \mathbf{\hbox{(Factorial de n) }} n! = n \cdot (n-1) \cdot (n-2) \cdots 2 \cdot 1 \hbox{ , } \forall n \in \mathbb{N}\\ \\ \mathbf{\hbox{(Propiedades)}} \left\{\begin{array}{l} n! = n \cdot (n-1)! \\ \\ 0! = 1 \\ \end{array}\right.\\ \\ \mathbf{\hbox{(Número combinatorio) }} \hbox{Dados n, m} \in \mathbb{N},n \geq m, \displaystyle{\binom{n}{m}} = \displaystyle{\frac{n!}{m!(n-m)!}} \\ \\ \mathbf{\hbox{(Propiedades)}} \left\{\begin{array}{l} \displaystyle{\binom{n}{0}} = 1, \displaystyle{\binom{n}{1}} = n, \displaystyle{\binom{n}{n}} = 1 \\ \\ \displaystyle{\binom{n}{m}} = \displaystyle{\binom{n}{n-m}} \\ \\ \displaystyle{\binom{n}{m}} + \displaystyle{\binom{n}{m+1}} = \displaystyle{\binom{n+1}{m+1}} \\ \end{array}\right.\\ \end{array}\right. $$

Triángulo de Tartaglia (o de Pascal)

$$ \left.\begin{array}{l} \left.\begin{array}{l} & & & & 1 & & & & \\ & & & 1 & & 1 & & & \\ & & 1 & & 2 & & 1 & & \\ & 1 & & 3 & & 3 & & 1 & \\ 1 & & 4 & & 6 & & 4 & & 1\\ & & & & \vdots & & & & \\ \end{array}\right. & \Leftrightarrow & \left.\begin{array}{l} & & & & \displaystyle{\binom{0}{0}} & & & & \\ & & & \displaystyle{\binom{1}{0}} & & \displaystyle{\binom{1}{1}} & & & \\ & & \displaystyle{\binom{2}{0}} & & \displaystyle{\binom{2}{1}} & & \displaystyle{\binom{2}{2}} & & \\ & \displaystyle{\binom{3}{0}} & & \displaystyle{\binom{3}{1}} & & \displaystyle{\binom{3}{2}} & & \displaystyle{\binom{3}{3}} & \\ \displaystyle{\binom{4}{0}} & & \displaystyle{\binom{4}{1}} & & \displaystyle{\binom{4}{2}} & & \displaystyle{\binom{4}{3}} & & \displaystyle{\binom{4}{4}}\\ & & & & \vdots & & & & \\ \end{array}\right.\\ \end{array}\right. $$

Combinatoria: Variaciones, Combinaciones y Permutaciones

$$ \left\{\begin{array}{l} \hbox{Importa el orden} \left\{\begin{array}{l} \hbox{No entran todos } \mathbf{\hbox{(Variaciones)}} \left\{\begin{array}{l} \hbox{Sin repetición: } V_{n,k}=\displaystyle{\frac{n!}{(n-k)!}}=n \cdot (n-1) \cdots (n-k+1)\\ \hbox{Con repetición: } VR_{n,k}=n^k \end{array}\right.\\ \\ \hbox{Entran todos } \mathbf{\hbox{(Permutaciones)}} \left\{\begin{array}{l} \hbox{Sin repetición: } P_n=n! = n \cdot (n-1) \cdot (n-2) \cdots 2 \cdot 1\\ \hbox{Con repetición: } PR_n^{\alpha_1,\alpha_2,\cdots,\alpha_k}=\displaystyle{\frac{n!}{\alpha_1! \cdot \alpha_2!\cdots \alpha_k!}} \end{array}\right.\\ \end{array}\right.\\ \\ \hbox{No importa el orden } \mathbf{\hbox{(Combinaciones)}} \left\{\begin{array}{l} \hbox{Sin repetición: } C_{n,k} = \displaystyle{\binom{n}{k}} = \displaystyle{\frac{n!}{(n-k)! \cdot k!}}\\ \hbox{Con repetición: } CR_{n,k} = C_{n+k-1,k} = \displaystyle{\binom{n+k-1}{k}} = \displaystyle{\frac{(n+k-1)!}{(n-1)! \cdot k!}}\\ \end{array}\right.\\ \end{array}\right. $$ $$ \left.\begin{array}{l} \mathbf{\hbox{ (Permutaciones circulares) }} PC_n=(n-1)!\\ \end{array}\right. $$

Actividades

Probabilidad

Sucesos y operaciones con sucesos

Cálculo de Probabilidades

Experiencias compuestas

Sistema completo de sucesos

Diagramas de árbol

Tablas de contingencia

Diagramas de Venn

Dados dos conjuntos A y B:

Dados tres conjuntos A, B y C:

Combinatoria

Números Combinatorios

Triángulo de Tartaglia (o de Pascal)

Combinatoria: Variaciones, Combinaciones y Permutaciones

Actividades y problemas (#1)

Actividades y problemas (#2)