$$\hbox{Distribución Normal Tipificada } \hbox{N(}0,1\hbox{)}$$

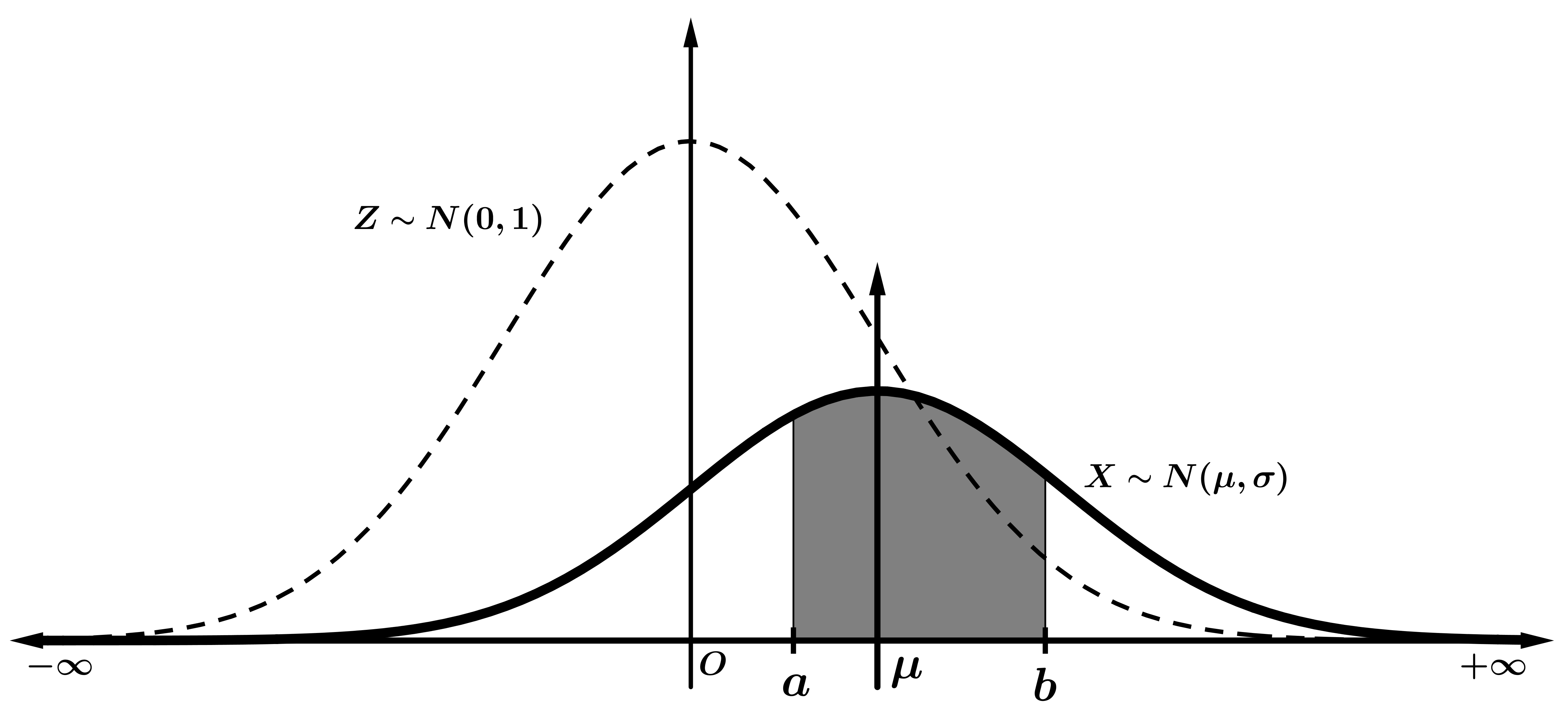
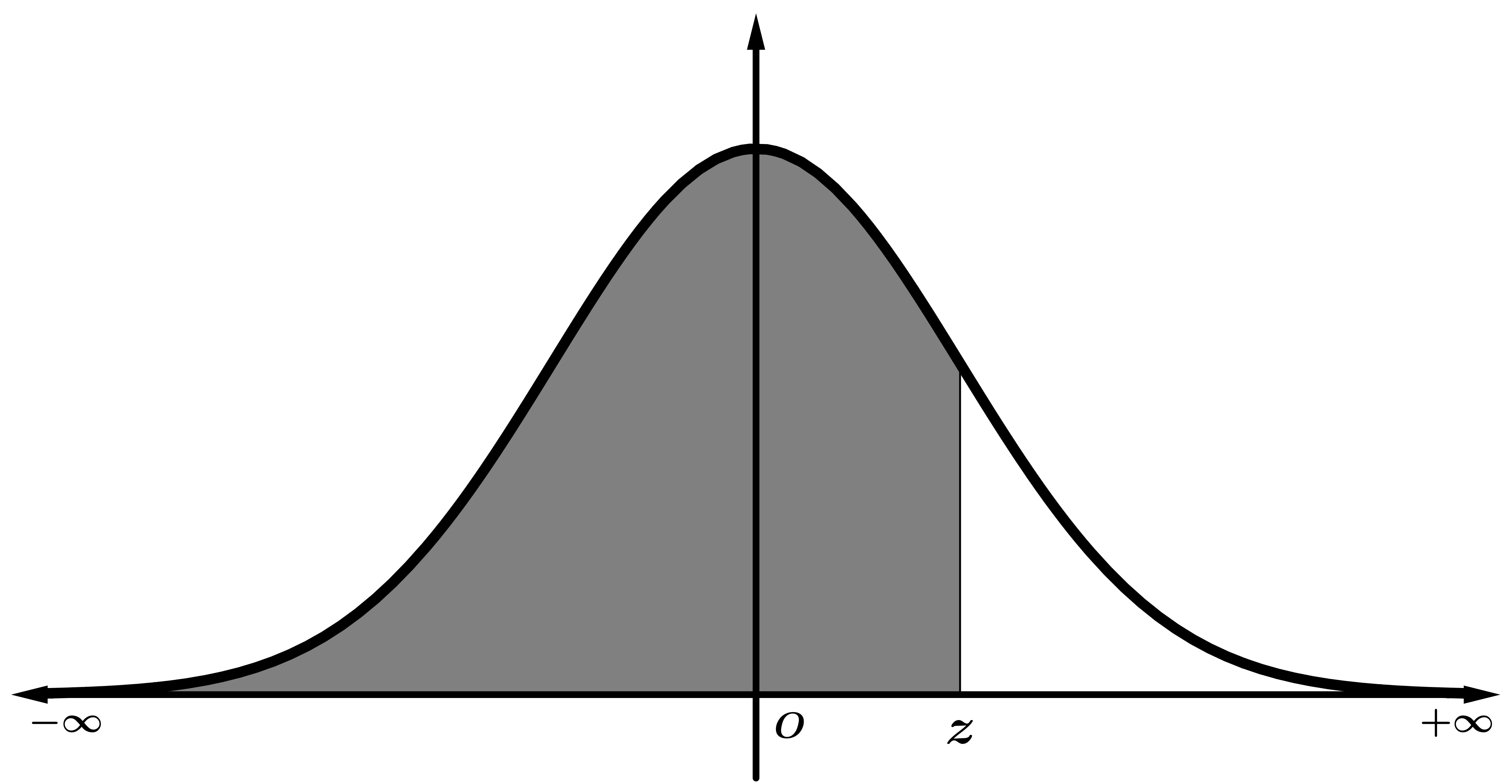
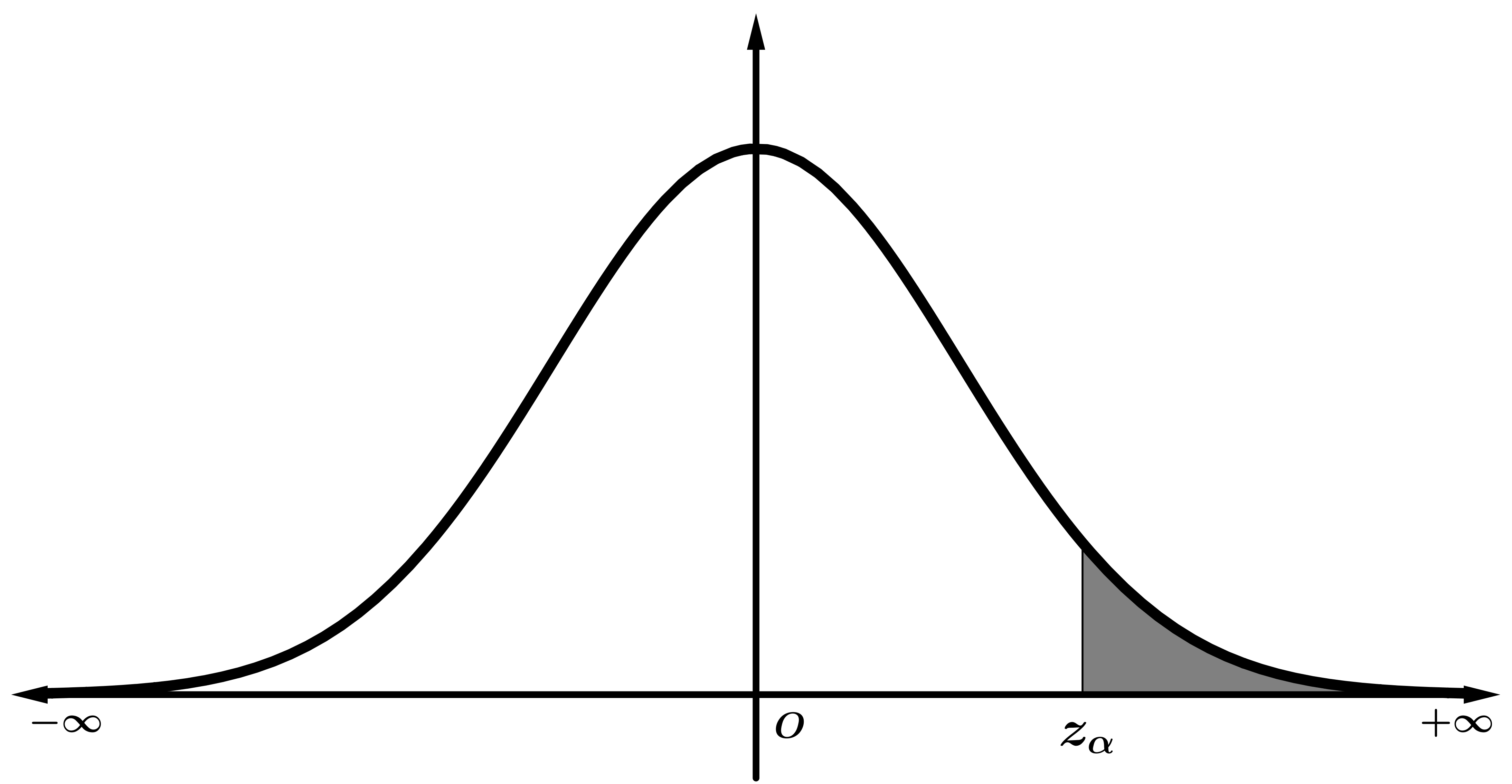
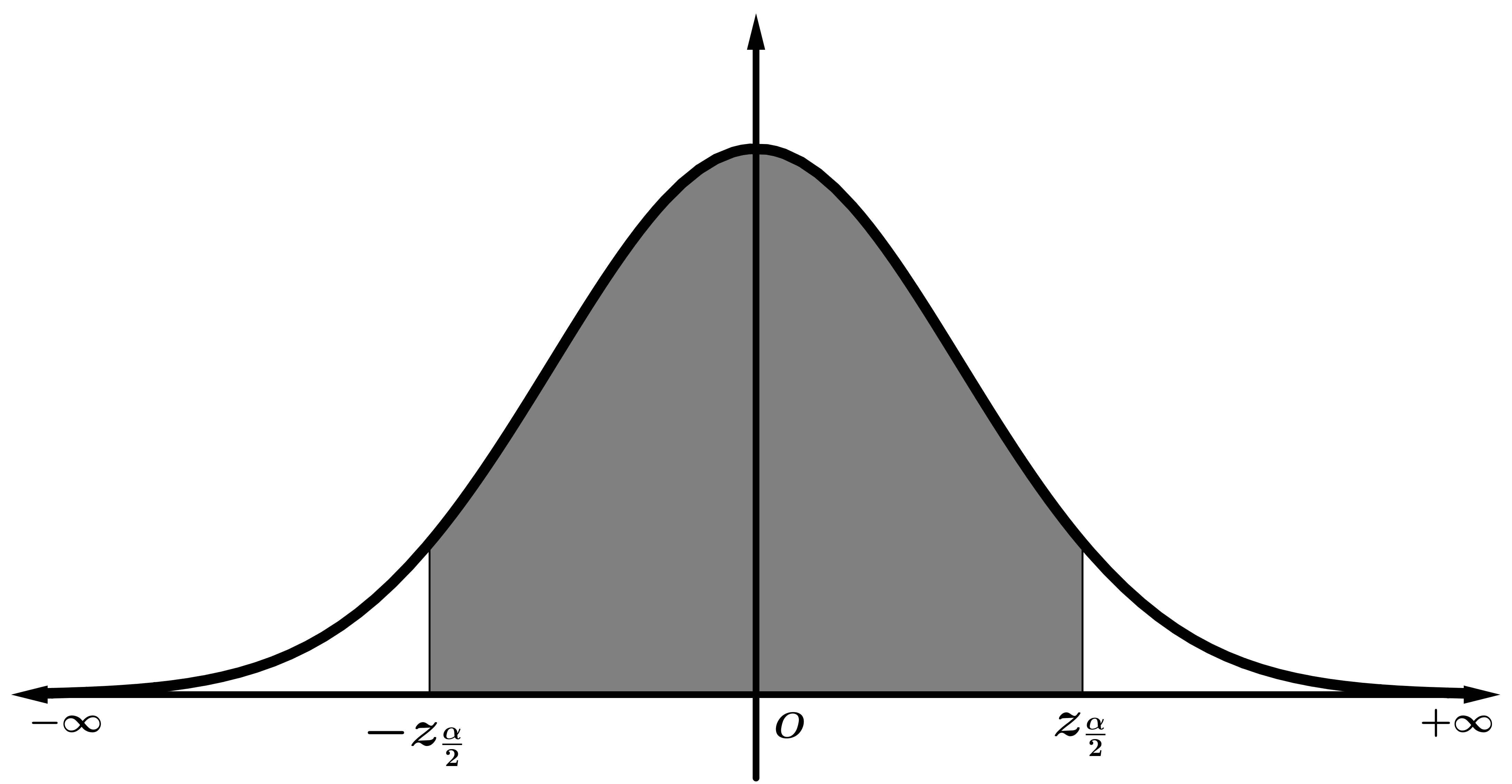
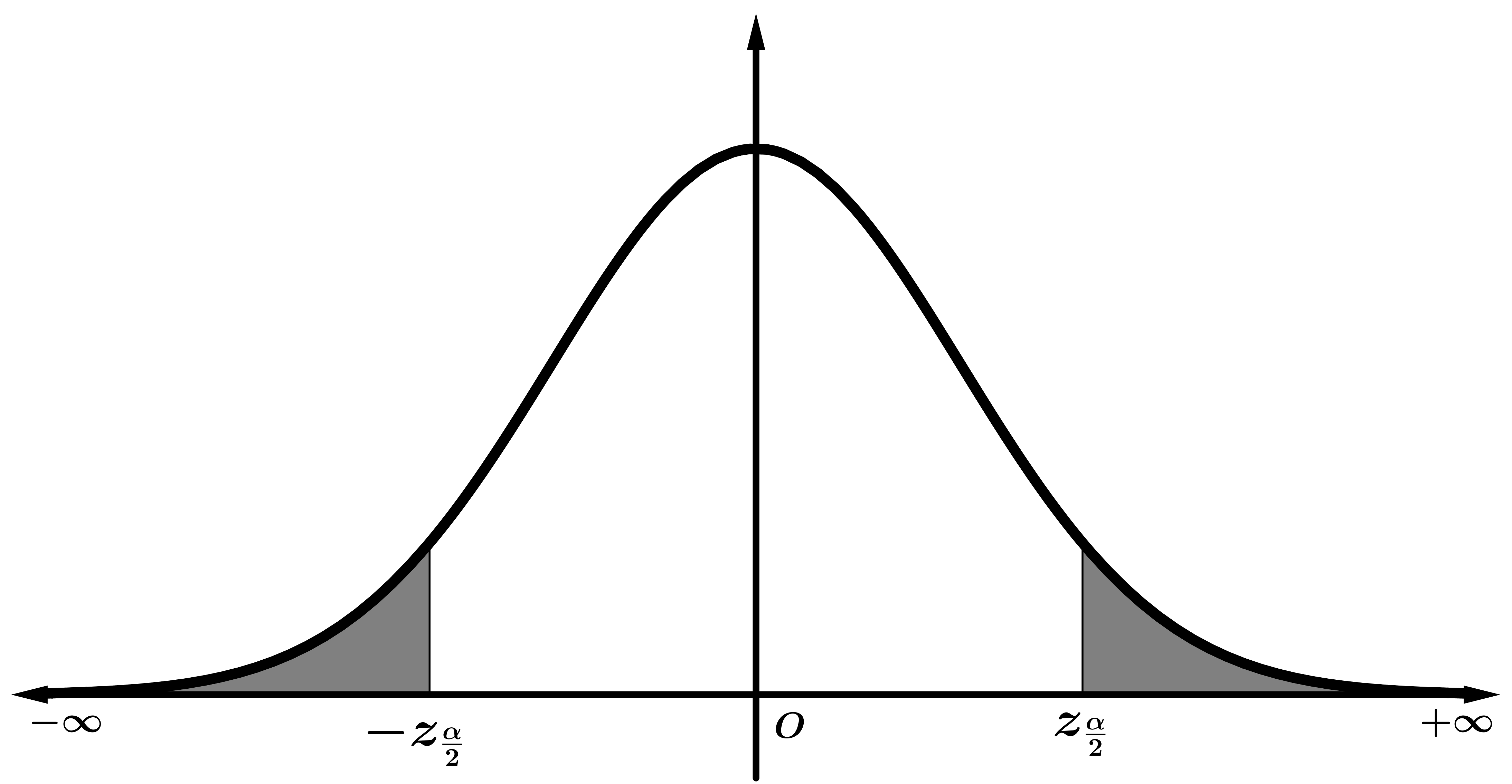
Área encerrada bajo la campana de Gauss y el eje X entre \( -\infty \) y z Valor crítico unilateral \( z_{\alpha} \) asociado a un nivel de significación \( \alpha \) $$p=P[Z \leq z]$$ $$\alpha=P[Z > z_{\alpha}]$$ Intervalo característico \((-z_{\frac{\alpha}{2}},z_{\frac{\alpha}{2}})\) asociado a un nivel de confianza \( p=1-\alpha\) Valor crítico bilateral \( z_{\frac{\alpha}{2}} \) asociado a un nivel de significación \( \alpha \) $$P[-z_{\frac{\alpha}{2}} \leq Z \leq z_{\frac{\alpha}{2}}]$$ $$\frac{\alpha}{2}=P[Z > z_{\frac{\alpha}{2}}]$$ \(z\) \(p\)

$$\hbox{Distribución Normal No Tipificada } \hbox{N(}\mu,\sigma\hbox{)}$$

$$p=P[a \leq X \leq b]$$

\(a\)	\(b\)	\(\mu\)	\(\sigma\)